Глава 4. Манипуляторы DIY

Рассмотренные в предыдущей главе модели деталей манипулятора являются составными частями собираемого манипулятора с угловой кинематикой. Таким образом, используя 3D принтер, можно выполнить печать всех необходимых конструктивных элементов углового манипулятора DIY, а затем собрать его. DIY — аббревиатура английского Do It Yourself, то есть — сделай сам.

Угловой манипулятор DIY

**Рис. 4.1. **Внешний вид манипулятора DIY с угловой кинематикой

Расчеты

Максимальная масса груза

Проведем оценку грузоподъемности робота. В рассматриваемой модели манипулятора применяются сервоприводы DYNAMIXEL XL431- T250-T и сервоприводы AR-S430-01, производимые OOO “Прикладная робототехника”. Их технические характеристики известны. Зная максимальный момент сервопривода, а также длины элементов конструкции модели, можно сделать расчет максимальной массы нагрузки, которую сможет поднять манипулятор.

В документации на сервоприводы можно найти, что максимальный момент, при котором сервоприводы способны к плавному и точному перемещению нагрузки – 0,53 Н∙м, а максимальный момент, который могут удерживать сервоприводы – 1,4 Н∙м.

Используя эти данные, рассчитаем массу полезной нагрузки для 2-го сервопривода в статическом положении, поскольку он является самым нагруженным из всех сервоприводов манипулятора. Первая степень в расчетах не учитывается, так как ось вращения вертикальна. Второму сервоприводу, помимо массы груза, также требуется перемещать массу всей конструкции манипулятора, которая расположена после него – то есть, 5 звеньев и 4 привода. Расчет будем проводить для самой нагруженной конфигурации манипулятора для второго сервопривода – горизонтальном положение, параллельно поверхности (рис. 4.2).

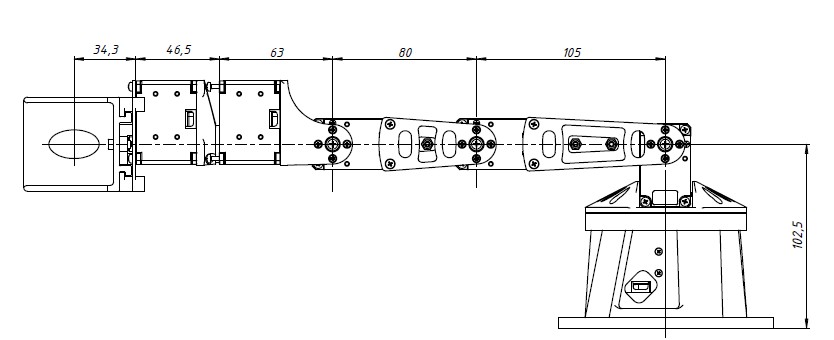
**Рис. 4.2. **Максимально нагруженное положение манипулятора

Формула для вычисления момента нагрузки на втрое звено имеет вид:

$K_{дин}$ - коэффициент динамики. Расчет производится для статического положения манипулятора, однако требуется учитывать динамические нагрузки. Стандартное значение $K_{дин}$ = 1,4.

$g$ - ускорение свободного падения.

$m_г$ - масса груза.

$l_м$ - расстояние до центра масс зацепа груза.

$m_{пр_i}$ - масса i-го сервопривода.

$l_{пр_i}$ - расстояние до центра масс i-го сервопривода.

$m_{зв_i}$ - масса i-го звена манипулятора.

$l_{зв_i}$ - расстояние до центра масс i-го звена манипулятора.

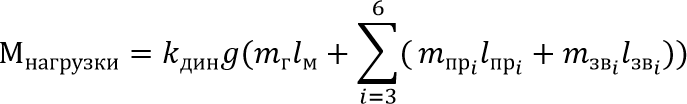
Примем расстояние до захватываемого груза 328,8 мм – длина от оси вращения второго сочленения до окончания схвата манипулятора.

$\displaystyle\sum_{i=3}^{6} m_{пр_i}$= 228 грамм - суммарная масса сервоприводов.

Для упрощения решения задачи будем считать, что центр масс сервопривода располагается в центре вала вращения. Таким образом, найдем плечо до каждого сервопривода от оси вращения второго сочленения (рис. 4.2).

Необходимую массу звеньев и центра масс узнаем с помощью модели в САП.

Масса звеньев робота зависит от формы, используемых материалов и технологии изготовлении. В случае использования стандартной модели звеньев манипулятора суммарная масса:

$\displaystyle\sum_{i=3}^{6} m_{зв_i}$=116грамма

Центр масс, учитывающий звенья третьей, четвертой, пятой и шестой степеней свободы, располагается на расстоянии 220 мм от оси вращения второго сервопривода.

Для нахождения массы груза с которым манипулятор имеет возможность взаимодействовать составим уравнение:

$$ M_{нагрузки}=M_{серв} $$

Таким образом момент, $M{нагрузки}$ создаваемый нагрузкой на второе сочленение, равняется моменту сервопривода $M{серв}$

$$M_{серв}=1,4Нм$$

Из электромеханической характеристики сервопривода найдем крутящий момент:

Приведем известные значения к системе СИ и подставим в формулу:

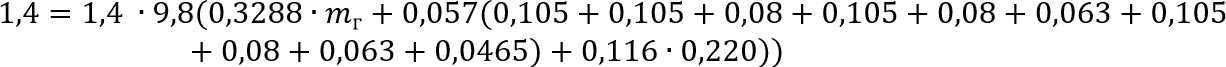
Преобразуем значения:

Выразим и найдем массу груза $m_г$:

Таким образом, максимальная масса груза для обеспечения нормальной работы манипулятора составляет 88 грамм. Однако, это приблизительный расчет, так как исследовалось статическое и наиболее нагруженное положение манипулятора.

Обратная задачи кинематики

Рассмотрим решение обратной задачи кинематики (ОЗК) для манипулятора с угловой кинематикой. Для исключения избыточных случаев можно принять положение выходного звена манипулятора вертикальным, при этом, захват будет все время находиться в вертикальном положении. В этом случае, ОЗК будет решаться однозначно.

Манипулятор можно условно разделить на 4 линейных сегмента с

соответствующими длинами l1,l2 ,l3 ,l4 . Причем, на первом и четвертом

звеньях находятся сервоприводы, дающие вращательную степень свободы вдоль продольной оси звена (Рис. 4.3).

Зеленым цветом показаны звенья манипулятора. Крестиками отмечены продольные степени вращения.

При данных условиях (звено 1 имеет только продольную степень вращения, расположено вертикально, звено 4 расположено вертикально, а 5-ый сервопривод также дает вертикальную степень вращения) можно абстрагироваться от всех звеньев манипулятора, и рассматривать только 2 и 3 звенья, перенеся ось координат в точку стыковки 1 и 2 звеньев, получив в результате ранее рассмотренный случай задачи кинематики (Рис.4.5).

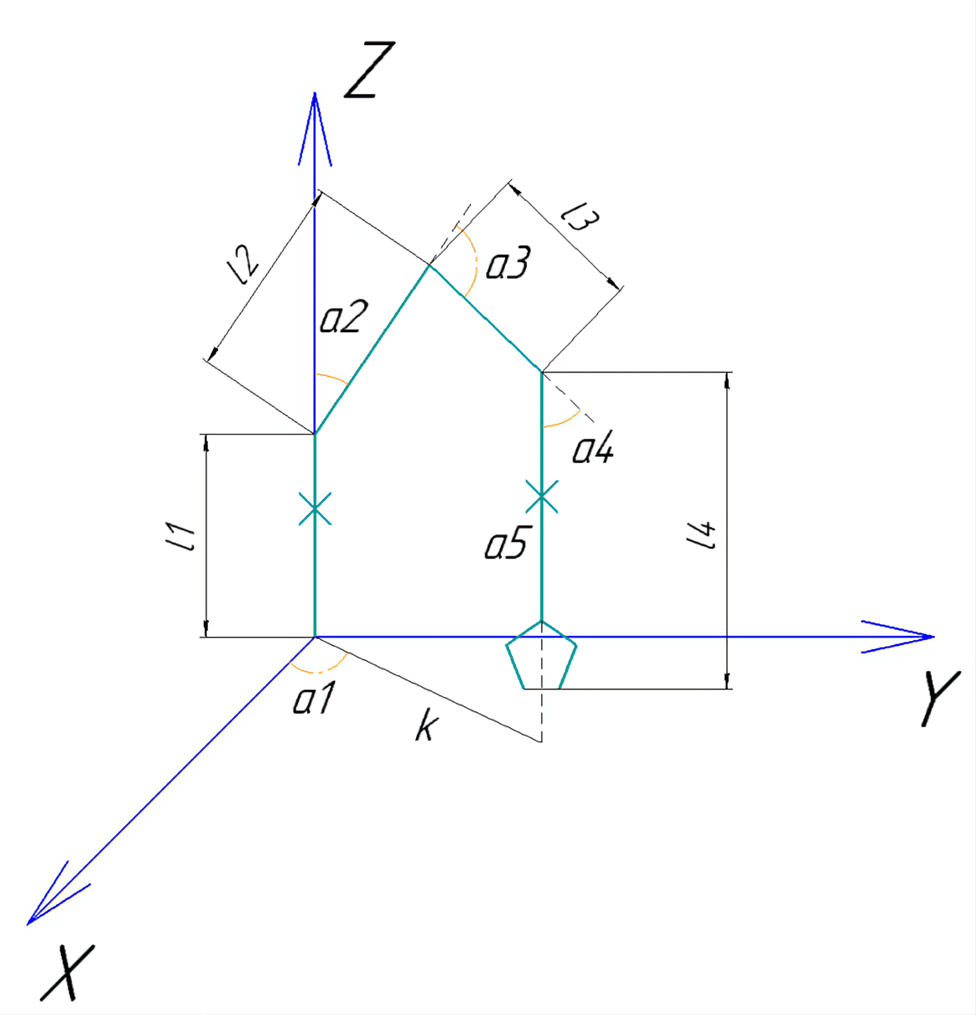
**Рис. 4.3. **Схема для решения обратной задачи кинематики

l1 = 102.50

l2 = 105

l3 = 80

l4 = 171.80

**Рис. 4.4. **Схема манипулятора

Обратная задача кинематики в данном случае будет решаться для точки А и относительно нововведенного начала координат, поэтому необходимо вычислить положение точки А относительно этого нового начала координат.

$z_{реш}=z+l_4-l_1$

**Рис. 4.5. **Приведение кинематической схемы к известной

$a_1=arctg(\frac{y}{x})$

$a_5=a_1$

$k=\sqrt {x^2+y^2}$

$d=\sqrt{k^2+z^2_p}$

$a_2=\frac {\pi}{2}-(arctg(\frac{z_p}{K})+arccos(\frac{d^2+l^2_2-l^2_3}{2dl_2}))$

$a_3=\pi-arccos(\frac{-d^2+l^2_2-l^2_3}{2l_2l_3})$

$a_4=\pi-(a_2+a_3)$

Разработка управляющей программы

Для программирования манипулятора с угловой кинематикой используется то же самое программное обеспечение и такой же набор аппаратных средств, которые использовались для программирования манипулятора с плоско-параллельной кинематикой, рассматриваемого в учебном пособии «СТЕМ Мастерская. Часть 1»

Чтение позиций сервоприводов

Для чтения позиций всех сервоприводов манипулятора с угловой кинематикой можно использовать следующий пример:

#include <Dynamixel2Arduino.h>

#define DXL_SERIAL Serial3 //Последовательный порт DXL платы OpenCM9.04 EXP. (Чтобы использовать порт DXL на плате OpenCM 9.04, используйте Serial1 для Serial. И из-за кода драйвера OpenCM 9.04 используйте Serial1.setDxlMode(true); перед dxl.begin();.)

#define DEBUG_SERIAL Serial // Установка константы, отвечающей за последовательный порт, подключаемый к компьютеру

const uint8_t DXL_DIR_PIN = 22; // ПИН-код DIR платы STEM Board (Чтобы использовать порт DXL на плате OpenCM 9.04, используйте 28 для PIN-кода DIR.)
const float DXL_PROTOCOL_VERSION = 2.0; // инициализация переменной, отвечающей за протокол передачи данных от OpenCM9.04 к сервоприводам

Dynamixel2Arduino dxl(DXL_SERIAL, DXL_DIR_PIN); // инициализация указателя на команды из библиотеки Dynamixel

#define jointN 6 // задание количества ненулевых столбцов массива #define pages 3 // задание количества ненулевых строк массива

int i=0;  // задание переменной-счетчика i

int j=1;  // задание переменной-счетчика j

int buf[pages+1][jointN+1]={ // инициализация двумерного массива, его размер задается: 3+1=4 на 6+1=7, 4 на 7, так как в программировании нумерация

{0,0, 0, 0, 0, 0, 0}, // элементов начинается с 0, но нулевой элемент мы использовать не будем, в связи с чем начнем с первого

{0, 507, 492, 531, 498, 521, 626, },

{0, 506, 443, 403, 385, 607, 626, },

{0, 508, 532, 627, 613, 412, 626, },

};

void setup() {

// поместите код установки здесь, чтобы запустить:

DEBUG_SERIAL.begin(57600); // установка скорости обмена данными по последовательному порту компьютера

dxl.begin(1000000);  // установка скорости обмена данными по последовательному порту манипулятора

dxl.setPortProtocolVersion(DXL_PROTOCOL_VERSION); // выбор протокола обмена данными

for (i=1; i<jointN+1; i++) // цикл с изменением i от 1 до 6 с шагом 1

{

dxl.setOperatingMode(i, OP_POSITION); // установка режима работы привода с номером i в качестве шарнира

}

}

void loop() {

// поместите свой основной код, чтобы запускать повторно:

for (j=1;j<=pages;j++) // цикл с изменением j от 1 до 6 с шагом 1

{

for(i=1;i<=jointN;i++) // цикл с изменением i от 1 до 6 с шагом 1

{

dxl.torqueOn(i); //подаем питание на i серву

dxl.setGoalVelocity(i, 50);  // задание целевой скорости 50 сервоприводу с номером i

dxl.setGoalPosition(i, buf[j][i]); // задание целевого положения, получаемого из элемента ([j],[i]) сервоприводу с номером i

}

delay(5000);

}

}

Данные после считывания будут выводиться на экран (в монитор порта) в заданном формате.

Воспроизведение записанных позиций

Далее рассматривается программа, позволяющая воспроизводить позиции, которые ранее были считаны предыдущей программой. С помощью этой программы можно достичь цели – переноса небольшого предмета из одной точки стола в другую.

#include <Dynamixel2Arduino.h> // подключение библиотеки Dynamixel

#define DXL_SERIAL Serial3 // Последовательный порт DXL платы OpenCM9.04 EXP. (Чтобы использовать порт DXL на плате OpenCM 9.04, используйте Serial1 для Serial. И из-за кода драйвера OpenCM 9.04 используйте Serial1.setDxlMode(true); перед dxl.begin();.)

#define DEBUG_SERIAL Serial // Установка константы, отвечающей за последовательный порт, подключаемый к компьютеру

const uint8_t DXL_DIR_PIN = 22; // инициализация переменной, отвечающей за номер пина, подключенного к информационному пину сервоприводов манипулятора

const float DXL_PROTOCOL_VERSION = 2.0; // инициализация переменной, отвечающей за протокол передачи данных от OpenCM9.04 к сервоприводам

Dynamixel2Arduino dxl(DXL_SERIAL, DXL_DIR_PIN); // инициализация указателя на команды из библиотеки Dynamixel

#define jointN 6  // инициализация константы, обозначающей количество сервоприводов (и, соответственно, элементов массива)

int pos=0;    // инициализация переменной
pos int i=0;  // инициализация переменной i

int buf[jointN+1];  // инициализация одномерного массива, его размер задается 6+1=7, так как в программировании нумерация

//  // элементов начинается с 0, но нулевой элемент мы использовать не будем, в связи с чем начнем с первого

//

void setup() {

//

/DEBUG_SERIAL.begin(57600); // установка скорости обмена данными по последовательному порту компьютера

dxl.begin(1000000);  // установка скорости обмена данными по последовательному порту манипулятора
dxl.setPortProtocolVersion(DXL_PROTOCOL_VERSION);  // выбор протокола обмена данными

for (i=1; i<jointN+1; i++) // цикл с изменением i от 1 до 6 с шагом 1

// {

dxl.setOperatingMode(i, OP_POSITION); // установка режима работы сервопривода с номером i в качестве шарнира

// }

//}

//

void loop() {

//

for (i=1; i<=jointN; i++) // цикл с изменением i от 1 до 6 с шагом 1

{

pos = dxl.getPresentPosition(i); // получение текущей позиции привода с номером i и запись в переменную pos

buf[i]=pos; // запись переменной значения pos в i-тый элемент массива buf

Serial.println(buf[i]);

}

Serial.print(«{0, «); //вывод в монитор порта текста «{0, «

for (i=1; i<=jointN; i++) // цикл с изменением i от 1 до 6 с шагом 1

{

Serial.print(buf[i]); // вывод в монитор порта значения ячейки массива с номером i

Serial.print(«, «); // вывод в монитор порта текста «, «

}

Serial.print(«}, «); // вывод в монитор порта текста «}, «

Serial.println(‘ ‘); // вывод в монитор порта текста « « и перенос курсора на следующую строку

//

delay(1000);  // задержка, пауза в 1 секунду

}

Обратите внимание, в этой программе задается двумерный массив, в котором записаны положения сервоприводов. Построчно записаны различные положения манипулятора, а по столбцам – отдельные положения каждого из сервоприводов. Поэтому массив имеет 6 столбцов и переменное количество строк, которое зависит от количества воспроизводимых положений (на самом деле, число строк и столбцов на 1 больше, так как есть неиспользуемые нулевые строка и столбец; они задаются нулевыми).

В основной части программы при помощи двух циклов перебираются элементы массива. Соответствующие значения отправляются на сервоприводы для воспроизведения, в результате чего манипулятор будет отрабатывать положения, заданные в массиве. Положения в массив будут предварительно записаны самим пользователем с использованием предыдущей программы.

Таким образом, 2 программы, работающие в связке, позволят организовать копирующий режим работы манипулятора. Данный режим в рассматриваемом примере работает следующим образом:

Считывание и вывод на экран позиций (используется программа для чтения позиций).

Затем человек вручную задает некоторую позицию манипулятора (поворачивая манипулятор рукой и придерживая его при этом). В монитор порта через каждую секунду выводится текущая конфигурация манипулятора. Когда значения построчно начинают повторяться, то есть манипулятор вручную установлен в целевую позицию, в мониторе порта необходимо выключить автопрокрутку, а затем, выделив курсором одну из нужных строчек (обозначающих целевую позицию), скопировать эту строку (используя связку горячих клавиш Ctrl+C). Далее эту строку необходимо будет вставить в программу для воспроизведения позиций.

Эти действия нужно повторять до тех пор, пока все позиции для воспроизведения не будут записаны.

Воспроизведение позиций.

Когда все позиции считаны и записаны в массив, необходимо убедиться, что программа работает корректно. Это можно сделать, проведя компиляцию. Также необходимо следить за тем, чтобы переменная, отвечающая за количество строк в массиве, была задана верно – под именно текущее количество строк (а оно зависит от пользователя).

Таким образом, предварительно «научив» манипулятор переносить какой-либо предмет (последовательно задавая все положения манипулятора, необходимые для переноса предмета: начальное, наведение на предмет, подход к предмету, схват, перенос, опускание предмета, отпускание предмета), можно добиться того, что манипулятор будет воспроизводить позиции, которым он ранее научился.

SCARA-манипулятор DIY

SCARA-манипуляторы представляют собой механизмы с рычажной кинематикой, рабочий орган которых перемещается в одной плоскости за счет вращательного движения рычагов, на конце которых он расположен. Как правило, такие манипуляторы состоят из двух рычагов, соединенных в одной точке и двух независимых приводов, один из которых находится в точке соединения рычагов и вращает их друг относительно друга. Второй же привод находится в точке крепления рычага к основанию и вращает его относительно рабочей плоскости. Внешний вид такого манипулятора представлен на рисунке 4.6:

**Рис. 4.6. **Типичный промышленный SCARA-манипулятор

Обратная задача кинематики SCARA-манипулятора

Для запуска манипулятора необходимо научиться решать обратную (инверсную) кинематическую задачу. Исходя из известной позиции, в которую требуется переместить манипулятор робота (например, схватить объект, который находится на конвейере в точке с координатами x, y) требуется определить величины углов, на которые необходимо повернуть двигатели, связанные с рычагами робота, чтобы установить его в правильное положение для захвата. Примеры положений звеньев манипулятора при достижении рабочим органом требуемого положения представлены на рисунке 4.7

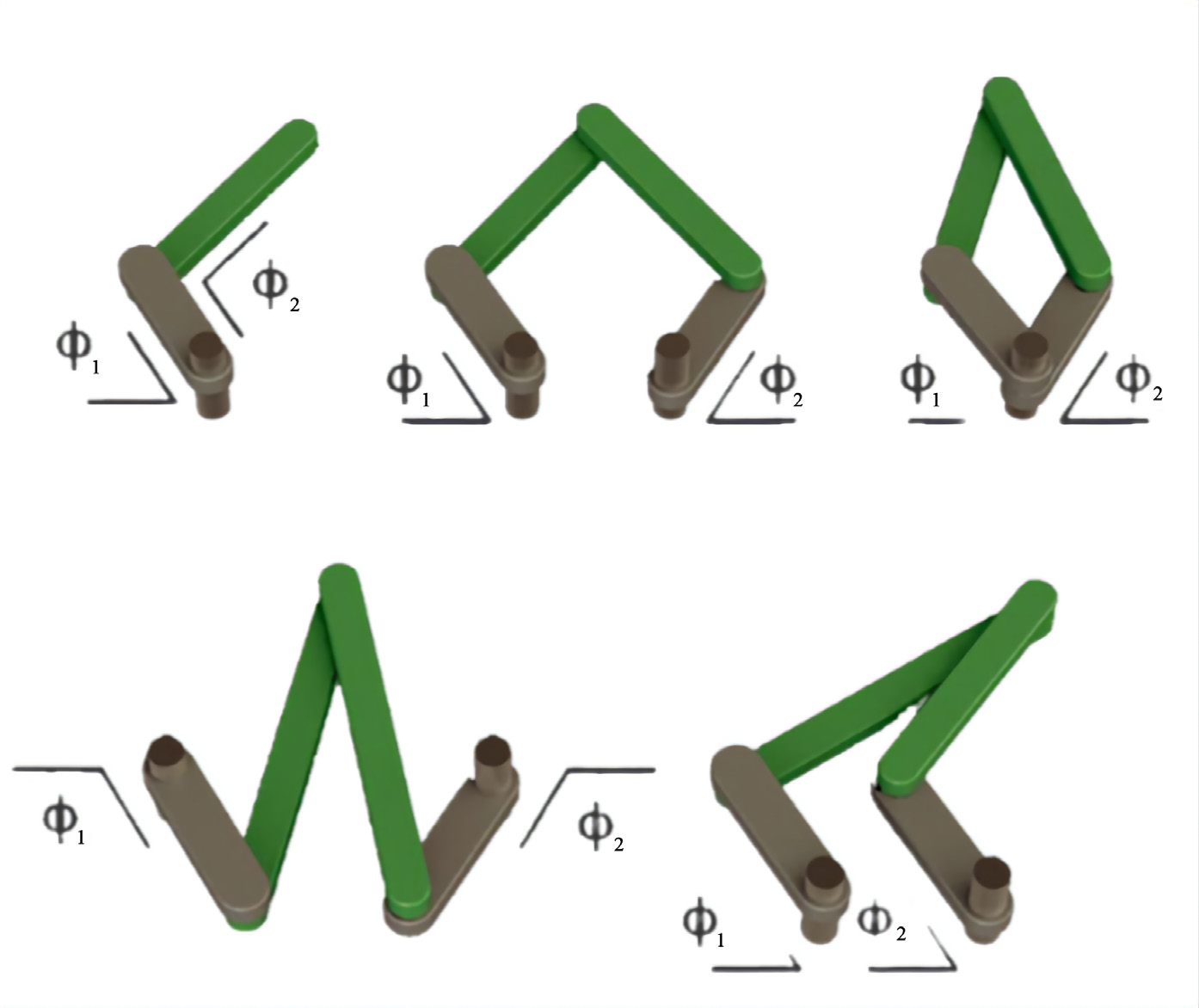
**Рис. 4.7. **Варианты положений рабочего органа манипулятора

Формализуем задачу: неподвижное основание и его движущиеся рычаги можно представить в виде отрезков, соединенных между собой шарнирами. Углы поворота рычагов робота обозначим как $0_1$, $0_2$,$0_3$ а координаты точек конца каждого рычага $Х_0,Х_1,Х_2 и Y_0, Y_1, Y_2,$ где в реальности будут закреплены сервопривода. Конечные координаты $Х_3$ и $Y_3$ нам известны. Это точка, в которую манипулятор должен прийти. Первый угол поворота рассматриваем от положительного направления оси Х до рычага. Последующие углы рассматриваются от предыдущего звена до рассматриваемого. Положительный угол поворота направлен против часовой стрелки.

Манипулятор SCARA имеет некоторую сложность с решением задачи. Это связано с тем, что для достижения конечной точки С могут способствовать различные положения манипулятора на плоскости.

**Рис. 4.8. **Возможность положения звеньев манипулятора при достижения конечной точки

В данном случае, механизм обладает избыточными степенями подвижности – движение звеньев может осуществляться при неподвижном схвате, что позволяет преодолевать внешние препятствия или проводить работы в замкнутых объемах. Поэтому для неподвижности конечного звена со схватом необходимо ввести еще одну координату γ – это угол, под которым конечное звено должно подойти к предмету относительно положительного направления оси Х. Таким образом, неопределенность будет возникать только между первым и вторым звеном манипулятора. Эта проблема решается программным способом.

**Рис. 4.9. **Варианты положений рабочего органа манипулятора

Для решения задачи введем несколько ключевых параметров, которые определяются геометрическими размерами робота: длины звеньев $l_1,l_2,l_3;$угол подхода схвата к объекту относительно оси Х, γ. Решение задачи осуществляется в программе MathCad. Зададим раз-

меры звеньев:

$l_1$ := 92

$l_2$ := 66

$l_3$ := 106

Укажем координаты, в которые должен прийти манипулятор, и угол, под которым он будет располагаться:

$x_3$ := 264

$y_3$ := 0

$\varphi$ := 0 deg

После того, как необходимые данные введены, можем начать решение.

1. Определим координаты конца второго звена:

$x_2:=x_3-l_3*cos(\varphi)$

$y_2:=y_3-l_3*sin(\varphi)$

2. Найдем координаты конца первого звена. Для этого составим систему уравнений двух окружностей. Центр координат первой окружности находится в начале системы координат (0,0), а её радиус равен длине первого звена l**1. Центр второй окружности находится в координатах конца второго звена (Х**2, Y2), а её радиус равен l**2. Найдем координаты пересечения этих двух окружностей. В результате получим квадратное уравнение и два корня. Приведем решение в программе MathCad:

$a:=x^2_2+l^2_1+y^2_2-l^2_2$

$D:=(4x_2a)^2-4*(-4y^2_2-4x^2_2)(-a^2+4l^2_1*y^2_2)=0$

$x_{11}:=\frac{(-4x_2a-\sqrt D)}{[2*(-4y^2_2-4x^2_2)]}=92$

$x_{12}:=\frac{(-4x_2a-\sqrt D)}{[2*(-4y^2_2-4x^2_2)]}=92$

В данном случае решение одинаковое, так как _D** _= 0, а пересечение окружностей осуществляется лишь в одной точке.

3. Теперь можно найти угол поворота первого звена для двух вариантов:

$fi_{11}:=a cos(\frac{x_11}{l_1}=0*deg)$

$fi_{12}:=a cos(\frac{x_12}{l_1}=0*deg)$

4. Найдем координаты $Y$ конца первого звена двух вариантов:

$y_{11}:=\sqrt {l^2_1-x^2_{11}}=0$

$y_{12}:=\sqrt {l^2_1-x^2_{12}}=0$

5. Далее рассчитаем длину проекции второго звена на оси:

$x_{21}:=x_2-x_{11}=66$ $x_{22}:=x_2-x_{12}=66$ $y_{21}:=y_2-y_{11}=66$ $y_{22}:=y_2-y_{12}=66$

6. Следующим шагом вычислим углы наклона проекции второго звена к оси Х:

$t_{21}:=a tan2(x_{21},y_{21})=0*deg$

$t_{22}:=a tan2(x_{22},y_{22})=0*deg$

Напомним, что данная функция определяется следующим образом:

$$ a tan2(a,b)= \begin{cases} arctg\frac{a}{b},b>0, \ arctg\frac{a}{b}+\pi,b>0,a>0,\ arctg\frac{a}{b}-\pi,b<0,a<0; \end{cases} $$

$$-\pi\leq a tan2(a,b)\leq\pi$$ Т.е. она учитывает принадлежность аргументов к одному из четырех квадрантов.

7. Определив разницу между углом наклона первого звена и второго, можно вычислить угол поворота второго звена относительно первого:

$fi_{21}:=t_{21}-fi_{11}=0deg$ $fi_{22}:=t_{22}-fi_{12}=0deg$ 8. Произведем рассчет для нахождения третьего угла поворота:

$fi_{31}:=\varphi-fi_{11}-fi_{21}$ $fi_{32}:=\varphi-fi_{12}-fi_{22}$

9. Необходимо сделать преобразование координат, поскольку наша декартовая система отличается от системы координат робота. Это связано с тем, что 0° для сервоприводов находится в другом положении от нашего представления. Координатная плоскость робота представлена на рис. 4.10.

Таким образом, обратная задача кинематики была решена. Теперь необходимо разработать систему управления манипулятором с использованием управляющего микроконтроллера.

**Рис. 4.10. **Координатная плоскость робота

Устройство SCARA-манипулятора

Инструкция по сборке робота, а также исходные файлы конструктивных элементов под лазерную резку находятся в свободном доступе и доступны для скачивания с официального сайта appliedrobotics.ru из раздела «Учебные материалы». Между каждым звеном установим три сервопривода. В качестве управляющего контроллера используется Arduino-подобная аппаратная платформа OpenCM, установленная на периферийной плате расширения STEM Board. Питание обеспечивается с помощью либо стандартного LiPo аккумулятора, выдающего номинальное напряжение в 11,1 В, либо через сетевой адаптер питания. Соединение сервоприводов рекомендуется выполнить последовательно и подключить получившуюся цепь к плате расширения, как на рисунке 4.11.

Также работ имеет подвижное конечно звено, которое перемещается в плоскости, перпендикулярной к основным звеньям. Оно будет управляться отдельно.

Перед тем, как приступить к разработке управляющей программы, необходимо уточнить ID сервоприводов, установленных на манипуляторе. ID сервоприводов указаны на рисунке 4.11.

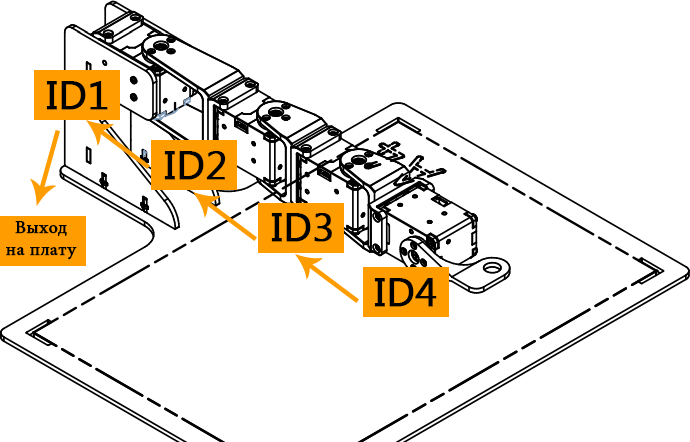
**Рис. 4.11. **Схема подключения сервоприводов и их ID

Для уточнения и установки ID сервоприводов можно использовать стандартные примеры из Arduino IDE с установленной поддержкой платы OpenCM9.04. Для этого необходимо открыть два примера под названием: “o_Find_Dynamixel” и “c_ID_Change”. (“Файл“ => “Примеры“ => OpenCM9.04 => DynamixelWorkbench).

С помощью примера “o_Find_Dynamixel” можно узнать текущее ID сервопривода следующим образом: сервопривод подключается к плате, подключается питание и загружается пример на плату. После чего в Мониторе порта можно увидеть информацию о текущем значении ID, которое необходимо запомнить.

После этого нужно открыть второй пример - “c_ID_Change”. В оглавлении, при необходимости, нужно изменить эти строки:

#define DXL_ID 1 // 1 – это текущее значение ID сервопривода
#define NEW_DXL_ID 2 // 2 – это значение, на которое требуется поменять ID

Помимо этого, в обоих случаях необходимо поменять скорость “общения” платы со входами Dynamixel

#define BAUDRATE 57600 // изменяем значение на 1 000 000

Таким образом, устанавливаются необходимые ID для сервоприводов.

Для обеспечения безопасной работы рекомендуется перед запуском определить, в каком положении находится вал сервопривода при 0°.

**Рис. 4.12. **SCARA-манипулятор

Разработка управляющей программы

В модели данного робота в качестве управляющего контроллера используется Arduino-подобный контроллер OpenCM. Для работы с ним используется среда разработки Arduino IDE.

Для работы с Dynamixel подключаем библиотеку и инициализируем переменные:

#include <DynamixelWorkbench.h>

Для обмена данных по протоколу Dynamixel в коде программы необходимо указать номер аппаратной шины – другими словами порты, на плате, к которым будет выполнено подключение сервоприводов.

#if defined( OPENCM904 )

#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-OpenCM 485EXP

#elif defined( OPENCR )
#define DEVICE_NAME «»
#endif

В рассматриваемом примере требуется выбрать 3 вариант Указываем скорость обмена данными через порт подключения

#define BAUDRATE 1000000 // Скорость передачи данных

Далее необходимо указать ID сервоприводов, которыми необходимо управлять. Все это делается в коде программы до функции setup() при помощи следующих команд:

#define DXL_ID1  1 // адрес сервопривода DYNAMIXEL
#define DXL_ID2  2
#define DXL_ID3  3
#define DXL_ID4  4

Инициализируем геометрические данные робота в качестве глобальных переменных. Они нам необходимы для расчетов. В рассматриваемой модели робота нужно проинициализировать следующие переменные:

DynamixelWorkbench dxl_wb;
float theta1, theta2, theta3;

float m = 0;
float n = 0;
float k= 0;
float t = 0;

float l1 = 92;
float l2 = 66;
float l3 = 106;

float x11;

bool flag = false;

Функция setup()

Зададим переменные model_number и присвоим им ID сервоприводов. После этого производим подключение всех сервоприводов манипулятора.

void setup() {
const char *log ;

Serial.begin(57600);

uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;

dxl_wb.init(DEVICE_NAME, BAUDRATE, &log);
dxl_wb.ping(DXL_ID1, &model_number1, &log);
dxl_wb.ping(DXL_ID2, &model_number2, &log);
dxl_wb.ping(DXL_ID3, &model_number3, &log);
dxl_wb.ping(DXL_ID4, &model_number4, &log);

dxl_wb.jointMode(DXL_ID1, 1, 1, &log);
dxl_wb.jointMode(DXL_ID2, 1, 1, &log);
dxl_wb.jointMode(DXL_ID3, 1, 1, &log);
dxl_wb.jointMode(DXL_ID4, 1, 1, &log);

}

Функция find_angle(float x, float y, float a)

В данной функции происходит решение обратной задачи. Входные данные:

x – координата схвата по оси Х y - координата схвата по оси Y

a – угол относительно оси Х, под которым необходимо, чтобы схват подошел к объекту

void find_angle(float x, float y, float a)

{

float x2 = x - l3*cos(a); // Нахождение координат конца второго звена
float y2 = y - l3*sin(a);

float d = sqrt(x2*x2 + y2*y2); // Введем параметр
if (d > (l1+l2)) // Проверка дискриминанта

{

Serial.println(«Out of zone»); // Если значение дискриминанта меньше нуля, манипулятор занимает базовое положение

theta1 = 0;
theta2 = 0;
theta3 = 0;

}

else

{

if (y < 0 && a <= 0 )

{

y = -y;
a = -a;
flag = true;

}

float A = ((l1*l1)-(l2*l2)+(d*d))/(d*2);
float alfa = acos(x2/d);

float delta = acos(A/l1);
float q1 = alfa - delta;
float x1 = l1*cos(q1);
float y1 = l1*sin(q1);

float q2 = acos((x2-x1)/l2);
theta1 = q1;

theta2 = q2-q1;
theta3 = a-q1-theta2;
if(flag)

{

Serial.println(«FLAG»);
theta1 = -theta1;
theta2 = -theta2;
theta3 = -theta3;

flag = false;

}

}

}

Функция set_pos()

В данной функции осуществляется задание угла поворота вала двигателя на манипуляторе

void set_pos( float p1 , float p2, float p3, float p4, int del)

// Функция для задания угла поворота вала двигателя на манипулятора в радианах

{

dxl_wb.goalPosition(DXL_ID1,p1);
dxl_wb.goalPosition(DXL_ID2,p2);
dxl_wb.goalPosition(DXL_ID3,p3);
dxl_wb.goalPosition(DXL_ID4,p4);
delay(del);

}

Функция loop()

Рассмотрим функцию loop(), которая представляет собой бесконечный цикл.

void loop() {

if (Serial.available() > 0 ) {

m = Serial.parseInt();

n = Serial.parseInt();
k = Serial.parseInt();

find_angle(m, n, k );
Serial.print(«Angle #1: « );
Serial.println(theta1*180/3.14);
Serial.print(«Angle #2: « );
Serial.println(theta2*180/3.14);
Serial.print(«Angle #3: « );
Serial.println(theta3*180/3.14);

}

set_pos(theta1, theta2, theta3, 0, 700); // Поворот валов приводов на вычисленный угол – достижение заданных координат

}

Также можно корректировать положения робота в реальном времени. С помощью консоли пользователь вручную может вводить координаты, которые будет занимать робот.

Координаты вводятся в миллиметрах. Значения можно вводить через любые знаки препинания, главное вводить их в правильном порядке и разделять пробелом.

В результате, код управляющей программы будет выглядеть следующим образом:

#include <DynamixelWorkbench.h>

#if defined( OPENCM904 )

#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-STEM Board

#elif defined( OPENCR )

#define DEVICE_NAME «»
#endif

#define BAUDRATE 1000000 // Скорость передачи данных
#define DXL_ID1 1 // адрес сервопривода DYNAMIXEL
#define DXL_ID2 2
#define DXL_ID3 3
#define DXL_ID4 4

DynamixelWorkbench dxl_wb;

float theta1, theta2, theta3;

float m = 0;
float n = 0;
float k= 0;
float t = 0;

float l1 = 92;
float l2 = 66;
float l3 = 106;

float x11;

bool flag = false;

void set_pos( float p1 , float p2, float p3, float p4, int del)

// Функция для задания угла поворота вала двигателя на манипулятора в радианах

{

dxl_wb.goalPosition(DXL_ID1,p1);
dxl_wb.goalPosition(DXL_ID2,p2);
dxl_wb.goalPosition(DXL_ID3,p3);
dxl_wb.goalPosition(DXL_ID4,p4);
delay(del);

}

void find_angle(float x, float y, float a)

{

float x2 = x - l3*cos(a);
float y2 = y - l3*sin(a);

float d = sqrt(x2*x2 + y2*y2);
if (d > (l1+l2))

{

Serial.println(«Out of zone»);
theta1 = 0;
theta2 = 0;
theta3 = 0;

}

else

{

if (y < 0 && a <= 0 )

{

y = -y;
a = -a;

flag = true;

}

float A = ((l1*l1)-(l2*l2)+(d*d))/(d*2);
float alfa = acos(x2/d);

float delta = acos(A/l1);

float q1 = alfa - delta;
float x1 = l1*cos(q1);
float y1 = l1*sin(q1);

float q2 = acos((x2-x1)/l2);

theta1 = q1;
theta2 = q2-q1;
theta3 = a-q1-theta2;

if(flag)

{

Serial.println(«FLAG»);
theta1 = -theta1;
theta2 = -theta2;
theta3 = -theta3;

flag = false;

}

}

}

void setup() {
const char *log ;

Serial.begin(57600);

uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;

dxl_wb.init(DEVICE_NAME, BAUDRATE, &log);
dxl_wb.ping(DXL_ID1, &model_number1, &log);
dxl_wb.ping(DXL_ID2, &model_number2, &log);
dxl_wb.ping(DXL_ID3, &model_number3, &log);
dxl_wb.ping(DXL_ID4, &model_number4, &log);

dxl_wb.jointMode(DXL_ID1, 1, 1, &log);
dxl_wb.jointMode(DXL_ID2, 1, 1, &log);
dxl_wb.jointMode(DXL_ID3, 1, 1, &log);
dxl_wb.jointMode(DXL_ID4, 1, 1, &log);

}

void loop() {

if (Serial.available() > 0 ) {

m = Serial.parseInt();
n = Serial.parseInt();
k = Serial.parseInt();
k = (k*3.14)/180;

find_angle(m, n, k );
Serial.print(«Angle #1: « );
Serial.println(theta1*180/3.14);
Serial.print(«Angle #2: « );
Serial.println(theta2*180/3.14);
Serial.print(«Angle #3: « );
Serial.println(theta3*180/3.14);

}

set_pos(theta1, theta2, theta3, 0, 700);

}

Таким образом, была решена обратная задача для плоского трехзвенного манипулятора, а также написана управляющая программа для реализации задачи на физической модели с микроконтроллером OpenCM.

STEWART-платформа DIY

STEWART - платформа (платформа Стюарта) представляет собой один из видов параллельного манипулятора, имеющего 6 степеней свободы. Отличительной особенностью данного вида манипуляторов является компоновка его сервоприводов – все сервопривода располагаются в одной плоскости тремя парами, что приводит к созданию шести тяг на шарнирных соединителях (Рис. 4.13).

Рабочий орган такого манипулятора чаще всего представляется в виде горизонтальной платформы, на котором размещается объект. За счет большого количества тяг становится возможно точное и быстрое изменение положения находящегося на платформе объекта в пространстве. Вследствие чего, платформы Стюарта используются в задачах, где необходимо точное позиционирование объекта в пространстве.

**Рис. 4.13. **Типовая модель платформы Стюарта

Обратная задача кинематики

Для запуска платформы необходимо научиться решать обратную (инверсную) кинематическую задачу. Исходя из требуемой позиции, в которую необходимо переместить платформу (например, для удержания в равновесии объекта, находящегося на платформе) требуется определить величины углов, на которые необходимо повернуть фланцы сервоприводов, связанные с тягами манипулятора, чтобы установить его платформу в правильное положение. Платформа является одним из видов параллельного манипулятора, имеющим шесть степеней свободы и координаты, по которым она может передвигаться линейное перемещение по осям $X,Y,Z,$ а также углы поворота: крен (Θ), тангаж (φ) и рысканье (ψ).

Манипулятор состоит из двух основных частей: неподвижной плоскости – базы, и подвижной плоскости – платформы. На базе находятся шесть сервоприводов, к фланцам которых прикреплены рычаги. В свою очередь, усилие от рычагов передается на тяги через шарнирные соединители, которые так же имеют шарнирное соединение с подвижной частью манипулятора.

Решение обратной задачи необходимо начать с размещения в центре основания точки отсчета системы координат с осями $х, у, z$. В таком случае, платформа будет иметь свою подвижную систему координат $х’,у’,z’$. Платформа определяется с помощью трех поступательных перемещений вдоль осей $х, у, z$ относительно основания. Три угла поворота вокруг осей определяют ориентацию платформы по отношению к основанию: поворот на угол $ψ$ вокруг оси $z$, поворот на угол $Θ$ вокруг оси $у$, поворот на угол $φ$ вокруг оси $х$.

Рассмотрим поворот относительно оси $z$ на угол $ψ$. Тогда матрица вращения $Rz(y)$ имеет вид:

$$ \begin{bmatrix} x \ y \ z \end{bmatrix} = R_Z(ψ) \begin{bmatrix} x' \ y' \ z' \end{bmatrix} $$

$$ R_z(ψ)=\begin{bmatrix} cosψ & -sinψ & 0\ sinψ & cosψ & 0\ 0 & 0 & 1 \end{bmatrix} $$

Аналогично, имеем матрицу вращения для поворота вокруг оси у на угол $Θ$:

$$ R_y(0)=\begin{bmatrix} cos0 & 0 & sin0\ 0 & 1 & 0\ -sin0 & 0 & cos0 \end{bmatrix} $$

Для третьего поворота на угол $φ$ вокруг оси $х$ имеем:

$$ R_z(ψ)=\begin{bmatrix} 1 & 0 & 0 \ 0 & cosφ & -sinφ\ 0 & sinφ & cosφ \end{bmatrix} $$

Полная матрица вращения платформы по отношению к основанию определяется по следующей формуле:

$$ {}^P R_B = R_z(\psi) \cdot R_y(\theta) \cdot R_x(\varphi) = $$

$$ \begin{pmatrix} \cos\psi & -\sin\psi & 0 \ \sin\psi & \cos\psi & 0 \ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos\theta & 0 & \sin\theta \ 0 & 1 & 0 \ -\sin\theta & 0 & \cos\theta \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \ 0 & \cos\varphi & -\sin\varphi \ 0 & \sin\varphi & \cos\varphi \end{pmatrix} $$

$$

\begin{pmatrix} \cos\psi \cos\theta & -\sin\psi & \cos\psi \sin\theta \ \sin\psi \cos\theta & \cos\psi & \sin\psi \sin\theta \ -\sin\theta & 0 & \cos\theta \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \ 0 & \cos\varphi & -\sin\varphi \ 0 & \sin\varphi & \cos\varphi \end{pmatrix} $$

$$

\begin{pmatrix} \cos\psi \cos\theta & -\sin\psi \cos\varphi + \cos\psi \sin\theta \sin\varphi & \sin\psi \sin\varphi + \cos\psi \sin\theta \cos\varphi \ \sin\psi \cos\theta & \cos\psi \cos\varphi + \sin\psi \sin\theta \sin\varphi & -\cos\psi \sin\varphi + \sin\psi \sin\theta \cos\varphi \ -\sin\theta & \cos\theta \sin\varphi & \cos\theta \cos\varphi \end{pmatrix} $$

Теперь рассмотрим i-тую тягу платформы Стюарта (Рис.4.14).

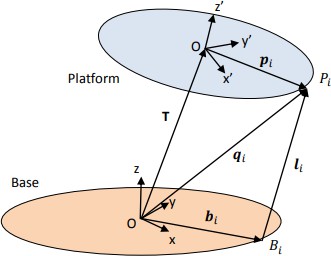
**Рис. 4.14. **Рассмотрение i-той тяги платоформы Стюарта

Координаты qi точки соединения верхней точки Pi относительно системы координат основания задаются уравнением:

$q_1=T+{}^pR_b*p_i$

Здесь вектор T описывает линейное перемещение начала координат платформы по отношению к системе координат основания, pi – является вектором, определяющим координаты точки соединения Pi относительно системы координат платформы.

Аналогичным образом задается длина i-ой тяги в следующем виде:

$l_i=T+{}^pR_b*p_i-b_i$

где bi – вектор, определяющий координаты нижней точки Bi соединения тяги. С помощью 6 уравнений определяют длины 6 тяг, таким образом, определяется положение и ориентация платформы.

Далее необходимо определить угол поворота вала сервопривода. При нахождении формулы использовались следующие обозначения (Рис. 4.15):

а – длина рычага сервопривода,

Аi – точки соединения рычага с нижней точкой стержня i-го сервопривода с координатами а = [xa, ya, za] в системе координат основания,

Вi – точки вращения центра рычага сервопривода с координатами b = [xb, yb, zb] в системе основания,

Pi – точки соединения верхнего шарнира стержня с платформой, с координатами р = [xр, yр, zр] в системе координат платформы,

S – длина стержня,

li = длина i-ого стержня,

α – угол между рычагом сервопривода и горизонталью,

β – угол между рычагом сервопривода и осью х После некоторых преобразований имеем:

$a=sin^-1\frac{L}{\sqrt M^2+N^2}-tan^-1\frac{N}{M}$

где

$$ L=l^2-(s^2-a^2) $$

$$ M=2a(z_p-z_b) $$

$$ N=2a[cos\beta(x_p-x_b)+sin\beta(y_p-_b)] $$

При расчете объявим все константы и приведем платформу в базовое положение, при котором все рычаги будут стоять параллельно базе.

$s := 211$ $\psi := 0 deg$ $x := 0$ $p := 110$ $е := 0 deg$ $y := 0$ $a := 35$ $\varphi := 0 deg$ $z := 200$ $b := 100$

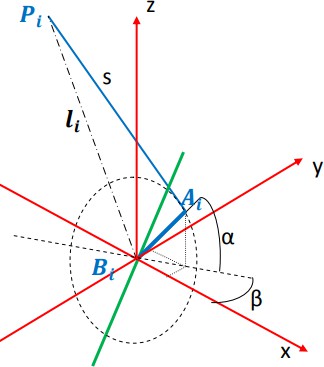**Рис. 4.15. **Схема расчета угла поворота вала сервопривода

Найдем проекции точек b и p на оси X и Y:

$b_{1x} := bcos(0.61) = 81.965$ $p_{1x} := pcos(0.13) = 109.072$ $b_{1y} := bsin(0.61) = 57.287$ $p_{1y} := psin(0.13) = 14.26$ $b_{2 x} := bcos(1.48) = 9.067$ $p_{2 x} := pcos(1.95) = -40.72$ $b_{2 y} := bsin(1.48) = 99.588$ $p_{2 y} := psin(1.95) = 102.186$ $b_{3x} := bcos(2.7) = -90.407$ $p_{3x} := pcos(2.22) = -66.501$ $b_{3 y} := bsin(2.7) = 42.738$ $p_{3 y} := psin(2.22) = 87.622$ $b_{4 x} := bcos(3.58) = -90.543$ $p_{4 x} := pcos(4.04) = -68.514$ $b_{4 y} := bsin(3.58) = -42.45$ $p_{4 y} := psin(4.04) = -86.057$ $b_{5x} := bcos(4.8) = 8.75$ $p_{5x} := pcos(4.31) = -43.078$ $b_{5 y} := bsin(4.8) = -99.616$ $p_{5 y} := psin(4.31) = -101.214$ $b_{6 x} := bcos(5.6) = 77.557$ $p_{6 x} := pcos(6.13) = 108.712$ $b_{6 y} := bcos(5.6) = -63.127$ $p_{6 y} := pcos(6.13) = -16.785$

Найдем матрицу поворота:

$$ R_i = \begin{pmatrix} \cos\psi \cos\theta & -\sin\psi \cos\varphi + \cos\psi \sin\theta \sin\varphi & \sin\psi \sin\varphi + \cos\psi \sin\theta \cos\varphi \ \sin\psi \cos\theta & \cos\psi \cos\varphi + \sin\psi \sin\theta \sin\varphi & -\cos\psi \sin\varphi + \sin\psi \sin\theta \cos\varphi \ -\sin\theta & \cos\theta \sin\varphi & \cos\theta \cos\varphi \end{pmatrix} $$

$$

\begin{pmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{pmatrix} $$

Найдем вектор l**1:

$$ \begin{pmatrix} x \ y \ z \end

R_i \begin{pmatrix} p_{lx} \ p_{ly}\ 0 \end

\begin{pmatrix} b_{lx} \ b_{ly} \ 0 \end

\begin{pmatrix} 27.107 \ -43.027 \ 200 \end{pmatrix} $$

Найдем длину вектора l**1:

$$ l = \sqrt{(27.1)^2 + (43)^2 + (200)^2} = 206.357 $$

Рассчитаем оставшиеся компоненты для конечной формулы:

$$ L := l^2 - (s^2 - a^2) = -712.59 $$

$$ M := 2a \cdot 1 = 1.445 \times 10^4 $$

$$ N := a * 2 \left[ \cos(0.61),(p_{lx} - b_{lx}) + \sin(0.61)*(p_{ly} - b_{ly}) \right] = -140.139 $$

$$ \alpha_i := a,sin!\left(\frac{L}{\sqrt{M^2 + N^2}}\right) - a,tan!\left(\frac{N}{M}\right) = -2.153deg $$

Небольшая ошибка присутствует из-за округлений и неточности измерения базовой высоты в 200 мм. Из-за конструкции в дальнейшем перед нечетными углами поворота необходимо ставить знак “ - ” для вращения в противоположную сторону.

Расчет для оставшихся пяти сервоприводов аналогичен.

Устройство платформы STEWART

Инструкция по сборке робота, а также исходные файлы конструктивных элементов под лазерную резку находятся в свободном доступе и доступны для скачивания с официального сайта appliedrobotics.ru из раздела «Учебные материалы». Сборка платформы Стюарта представляет собой размещение 6 сервоприводов на базе, установке на их фланцы рычагов и соединение подвижной платформы с рычагами через тяги с использованием шарнирного соединения. Перед установкой рычага необходимо перевести сервопривода в нулевое положение и присоединить рычаг параллельно базе. Также необходимо обратить внимание, что соседние рычаги располагаются навстречу друг другу в базовом положении. Тяги должны располагаться, как показано на рисунке 4.15.

В качестве управляющего контроллера используется Arduino-подобная аппаратная платформа OpenCM, установленная совместно со встраиваемой платой NanoPi-AR на плате расширения STEM Board. Питание обеспечивается либо при помощи стандартного LiPo аккумулятора, выдающего номинальное напряжение в 11,1 В, либо через сетевой адаптер питания. Соединение сервоприводов рекомендуется выполнить последовательно и подключить получившуюся цепь к плате расширения STEM Board как показано на Рис. 4.16.

Перед тем как приступить к разработке управляющей программы, необходимо уточнить ID сервоприводов, установленных на манипуляторе. ID сервоприводов указаны на следующей схеме, приведенной на рисунке 4.16.

Для уточнения и установки ID сервоприводов можно использовать стандартные примеры из Arduino IDE с установленной поддержкой платы OpenCM9.04. Для этого необходимо открыть два примера под названием: “oFind_Dynamixel” и “c_ID_Change”. (“Файл“ => “Примеры“ => OpenCM9.04 => DynamixelWorkbench). С помощью примера “o_Find Dynamixel” можно узнать текущее ID сервопривода следующим образом: сервопривод подключается к плате, к нему подключается питание, после чего на контроллер загружается пример. После чего в Мониторе порта сможем увидеть информацию о текущем значении ID, которое необходимо запомнить.

Теперь необходимо открыть второй пример “c_ID_Change”. В оглавлении, при необходимости, нужно изменить эти строки:

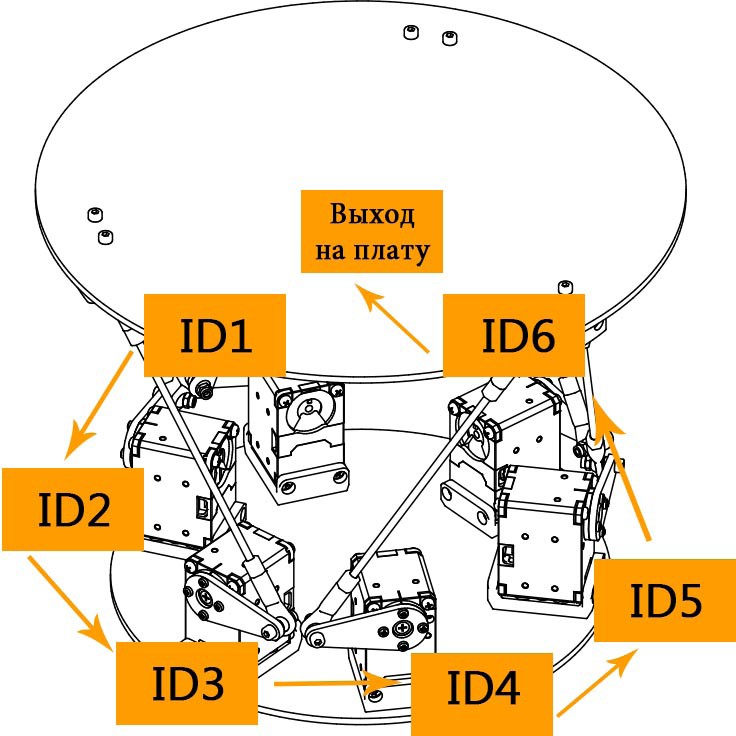
**Рис. 4.16. **Схема подключения сервоприводов и их ID

#define DXL_ID 1 // 1 – это текущее значение ID сервопривода #define NEW_DXL_ID 2 // 2 – это значение, на которое требуется поменять ID

Помимо этого, в обоих случаях необходимо поменять скорость “общения” платы со входами DYNAMIXEL.

#define BAUDRATE 57600 // изменяем значение на 1 000 000 Таким образом, устанавливаются необходимые ID для сервоприводов.

Для обеспечения безопасной работы, рекомендуется перед запуском определить, в каком положении находится вал сервопривода в положении 0°.

Разработка управляющей программы

В модели данного робота в качестве управляющего контроллера используется контроллер OpenCM. Для работы с ним используется среда разработки Arduino IDE.

Для работы с Dynamixel подключаем библиотеку и инициализируем переменные:

#include <DynamixelWorkbench.h>

После чего подключаем библиотеку для работы с математическими выражениями

#include <math.h>

Для обмена данных по протоколу Dynamixel в коде программы необходимо указать аппаратную шину. Другими словами, порты на плате, к которым будет выполнено подключение сервоприводов.

#if defined( OPENCM904 )

#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-OpenCM 485EXP

#elif defined( OPENCR )
#define DEVICE_NAME «»
#endif

Указываем скорость обмена данными через порт подключения:

#define BAUDRATE 1000000

Далее необходимо указать ID сервоприводов, которыми необходимо управлять. Все это делается в коде программы до функции setup() при помощи следующих команд:

#define DXL_ID1 1

#define DXL_ID2 2

#define DXL_ID3 3

#define DXL_ID4 4

#define DXL_ID5 5

#define DXL_ID6 6
DynamixelWorkbench dxl_wb;

Инициализируем геометрические данные робота в качестве глобальных переменных. Они нам необходимы для расчетов. В рассматриваемой модели робота инициализируем следующие переменные:

float s = 211;
float a = 35;
float b = 100;
float p = 110;
float fi_b = 0.61;
float fi_p = 0.13;

float bx, by, px, py;
float R[3][3];

float alfa1 = 0;
float beta1 = 0;
float gama1 = 0;
float x1;

float y_1;
float z1;

float angle0, angle1, angle2, angle3,angle4, angle5, angle6;

Функция setup()

Создаем переменные model_number и присваиваем им номер сервопривода. После производим подключение всех сервоприводов манипулятора.

void setup()

{

const char *log ;
Serial.begin(1000000);
uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;
uint16_t model_number5 = 5;
uint16_t model_number6 = 6;

dxl_wb.init(DEVICE_NAME, BAUDRATE, &log); dxl_wb.ping(DXL_ID1, &model_number1, &log); dxl_wb.ping(DXL_ID2, &model_number2, &log); dxl_wb.ping(DXL_ID3, &model_number3, &log); dxl_wb.ping(DXL_ID4, &model_number4, &log); dxl_wb.ping(DXL_ID5, &model_number5, &log); dxl_wb.ping(DXL_ID6, &model_number6, &log);

dxl_wb.jointMode(DXL_ID1, 20, 20, &log);
dxl_wb.jointMode(DXL_ID2, 20, 20, &log);
dxl_wb.jointMode(DXL_ID3, 20, 20, &log);
dxl_wb.jointMode(DXL_ID4, 20, 20, &log);
dxl_wb.jointMode(DXL_ID5, 20, 20, &log);
dxl_wb.jointMode(DXL_ID6, 20, 20, &log);

}

Теперь рассмотрим действие каждой функции отдельно.

Функция matrix(float alfa, float beta, float gama)

В данной функции находится матрица поворота, которая соответствует уравнению:

void matrix(float alfa, float beta, float gama)

{

R[0][0] = cos(alfa)*cos(beta);

R[1][0] = -sin(alfa)*cos(gama) + cos(alfa)*sin(beta)*sin(gama); R[2][0] = sin(alfa)*sin(gama) + cos(alfa)*sin(beta)*cos(gama); R[0][1] = sin(alfa)*cos(beta);

R[1][1] = cos(alfa)*cos(gama) + sin(alfa)*sin(beta)*sin(gama); R[2][1] = -cos(alfa)*sin(gama) + sin(alfa)*sin(beta)*cos(gama); R[0][2] = -sin(beta);

$$ R_i = \begin{pmatrix} \cos\psi \cos\theta & -\sin\psi \cos\varphi + \cos\psi \sin\theta \sin\varphi & \sin\psi \sin\varphi + \cos\psi \sin\theta \cos\varphi \ \sin\psi \cos\theta & \cos\psi \cos\varphi + \sin\psi \sin\theta \sin\varphi & -\cos\psi \sin\varphi + \sin\psi \sin\theta \cos\varphi \ -\sin\theta & \cos\theta \sin\varphi & \cos\theta \cos\varphi \end

\begin{pmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{pmatrix} $$

R[1][2] = cos(beta)*sin(gama);
R[2][2] = cos(beta)*cos(gama);

}

Функция angle(float fi_b, float fi_p, float x, float y, float z)

При помощи данной функции можно определить угол поворота для i-го рычага

void angle(float fi_b, float fi_p, float x, float y, float z)

{

bx = b*cos(fi_b);
by = b*sin(fi_b);
px = p*cos(fi_p);
py = p*sin(fi_p);

float A = R[0][0]*px + R[1][0]*py;

float B = R[0][1]*px + R[1][1]*py;

float C = R[0][2]*px + R[1][2]*py ;

A = A - bx + x;

B = B - by + y;

C = C + z;

float l = sqrt(A*A + B*B + C*C);
float L = l*l - s*s + a*a;

float M = 2*a*l;

float N = 2*a*(cos(fi_b)*(px - bx) + sin(fi_b)*(py - by));
angle0 = -(asin(L/(sqrt(M*M + N*N))) - atan(N/M));

}

Функция set_pos(float p1 , float p2, float p3, float p4, float p5, float p6,int del)

В данной функции осуществляется задание угла поворота вала двигателя на манипуляторе

void set_pos( float p1 , float p2, float p3, float p4, float p5, float p6, int del)

{

dxl_wb.goalPosition(DXL_ID1,p1); dxl_wb.goalPosition(DXL_ID2,p2); dxl_wb.goalPosition(DXL_ID3,p3); dxl_wb.goalPosition(DXL_ID4,p4); dxl_wb.goalPosition(DXL_ID5,p5); dxl_wb.goalPosition(DXL_ID6,p6);
delay(del);

}

Функция loop()

Теперь рассмотрим функцию loop(), которая представляет собой бесконечный цикл. Через нее можно корректировать положения робота в реальном времени. С помощью консоли пользователь может вручную вводить координаты, которые будет занимать робот.

void loop()

{

if (Serial.available() > 0 ) {
x1 = Serial.parseInt();
y_1 = Serial.parseInt();
z1 = Serial.parseInt();
alfa1 = Serial.parseInt();
beta1 = Serial.parseInt();

gama1 = Serial.parseInt();
Serial.print(«X = « );
Serial.println(x1);
Serial.print(«Y = « );
Serial.println(y_1);
Serial.print(«Z = « );
Serial.println(z1);
Serial.print(«Alfa = « ); Serial.println(alfa1);
Serial.print(«Beta = « ); Serial.println(beta1);
Serial.print(«Gamma = « ); Serial.println(gama1);
alfa1 = alfa1*3.14/180;
beta1 = beta1*3.14/180;

gama1 = gama1*3.14/180;
matrix(alfa1, beta1, gama1);

angle(0.61, 0.13, x1, y_1, z1);
angle1 = angle0;

angle(1.48, 1.95, x1, y_1, z1);

angle2 = -angle0;

angle(2.7, 2.22, x1, y_1, z1);
angle3 = angle0;

angle(3.58, 4.04, x1, y_1, z1);
angle4 = -angle0;

angle(4.8, 4.31, x1, y_1, z1);
angle5 = angle0;

angle(5.6, 6.13, x1, y_1, z1);
angle6 = -angle0;

Serial.print(«Angle #1: « ); Serial.println(angle1);
Serial.print(«Angle #2: « ); Serial.println(angle2);
Serial.print(«Angle #3: « ); Serial.println(angle3);
Serial.print(«Angle #4: « ); Serial.println(angle4);
Serial.print(«Angle #5: « ); Serial.println(angle5);
Serial.print(«Angle #6: « ); Serial.println(angle6);

set_pos(angle1, angle2, angle3, angle4, angle5, angle6, 50);

}

}

Координаты вводятся в миллиметрах. Значения можно вводить через любые знаки препинания, но в правильном порядке, и разделяя их пробелом.

В результате, код управляющей программы будет выглядеть следующим образом:

#include <DynamixelWorkbench.h>
#include <math.h>

#if defined( OPENCM904 )

#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-OpenCM 485EXP

#elif defined( OPENCR )
#define DEVICE_NAME «» #endif

#define BAUDRATE 1000000

#define DXL_ID1 1

#define DXL_ID2 2

#define DXL_ID3 3

#define DXL_ID4 4

#define DXL_ID5 5

#define DXL_ID6 6
DynamixelWorkbench dxl_wb;

float s = 211;
float a = 35;
float b = 100;
float p = 110;
float fi_b = 0.61;
float fi_p = 0.13;

float bx, by, px, py;
float R[3][3];

float alfa1 = 0;
float beta1 = 0;
float gama1 = 0;
float x1;

float y_1;
float z1;

float angle0, angle1, angle2, angle3, angle4, angle5, angle6;

void set_pos( float p1 , float p2, float p3, float p4, float p5, float p6, int del)

{

dxl_wb.goalPosition(DXL_ID1,p1);
dxl_wb.goalPosition(DXL_ID2,p2);
dxl_wb.goalPosition(DXL_ID3,p3);
dxl_wb.goalPosition(DXL_ID4,p4);
dxl_wb.goalPosition(DXL_ID5,p5);
dxl_wb.goalPosition(DXL_ID6,p6);
delay(del);

}

void matrix(float alfa, float beta, float gama)

{

R[0][0] = cos(alfa)*cos(beta);

R[1][0] = -sin(alfa)*cos(gama) + cos(alfa)*sin(beta)*sin(gama);
R[2][0] = sin(alfa)*sin(gama) + cos(alfa)*sin(beta)*cos(gama);
R[0][1] = sin(alfa)*cos(beta);

R[1][1] = cos(alfa)*cos(gama) + sin(alfa)*sin(beta)*sin(gama);
R[2][1] = -cos(alfa)*sin(gama) + sin(alfa)*sin(beta)*cos(gama);
R[0][2] = -sin(beta);

R[1][2] = cos(beta)*sin(gama);

R[2][2] = cos(beta)*cos(gama);

}

void angle(float fi_b, float fi_p, float x, float y, float z)

{

bx = b*cos(fi_b);
by = b*sin(fi_b);
px = p*cos(fi_p);
py = p*sin(fi_p);

float A = R[0][0]*px + R[1][0]*py;

float B = R[0][1]*px + R[1][1]*py;

float C = R[0][2]*px + R[1][2]*py ;

A = A - bx + x;

B = B - by + y;

C = C + z;

float l = sqrt(A*A + B*B + C*C);
float L = l*l - s*s + a*a;

float M = 2*a*l;

float N = 2*a*(cos(fi_b)*(px - bx) + sin(fi_b)*(py - by));
angle0 = -(asin(L/(sqrt(M*M + N*N))) - atan(N/M));

}

void setup()

{

const char *log ;
Serial.begin(1000000);
uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;
uint16_t model_number5 = 5;
uint16_t model_number6 = 6;

dxl_wb.init(DEVICE_NAME, BAUDRATE, &log);
dxl_wb.ping(DXL_ID1, &model_number1, &log);
dxl_wb.ping(DXL_ID2, &model_number2, &log);
dxl_wb.ping(DXL_ID3, &model_number3, &log);
dxl_wb.ping(DXL_ID4, &model_number4, &log);
dxl_wb.ping(DXL_ID5, &model_number5, &log);
dxl_wb.ping(DXL_ID6, &model_number6, &log);

dxl_wb.jointMode(DXL_ID1, 20, 20, &log);
dxl_wb.jointMode(DXL_ID2, 20, 20, &log);
dxl_wb.jointMode(DXL_ID3, 20, 20, &log);
dxl_wb.jointMode(DXL_ID4, 20, 20, &log);
dxl_wb.jointMode(DXL_ID5, 20, 20, &log);
dxl_wb.jointMode(DXL_ID6, 20, 20, &log);

}

void loop()

{

if (Serial.available() > 0 ) {
x1 = Serial.parseInt();
y_1 = Serial.parseInt();
z1 = Serial.parseInt();
alfa1 = Serial.parseInt();
beta1 = Serial.parseInt();

gama1 = Serial.parseInt();
Serial.print(«X = « );
Serial.println(x1);
Serial.print(«Y = « );
Serial.println(y_1);
Serial.print(«Z = « );
Serial.println(z1);
Serial.print(«Alfa = « );
Serial.println(alfa1);
Serial.print(«Beta = « );
Serial.println(beta1);
Serial.print(«Gamma = « );
Serial.println(gama1);

alfa1 = alfa1*3.14/180;
beta1 = beta1*3.14/180;

gama1 = gama1*3.14/180;
matrix(alfa1, beta1, gama1);

angle(0.61, 0.13, x1, y_1, z1);
angle1 = angle0;

angle(1.48, 1.95, x1, y_1, z1);
angle2 = -angle0;

angle(2.7, 2.22, x1, y_1, z1);
angle3 = angle0;

angle(3.58, 4.04, x1, y_1, z1);
angle4 = -angle0;

angle(4.8, 4.31, x1, y_1, z1);
angle5 = angle0;

angle(5.6, 6.13, x1, y_1, z1);
angle6 = -angle0;

Serial.print(«Angle #1: « );
Serial.println(angle1);
Serial.print(«Angle #2: « );
Serial.println(angle2);
Serial.print(«Angle #3: « );
Serial.println(angle3);
Serial.print(«Angle #4: « );
Serial.println(angle4);
Serial.print(«Angle #5: « );
Serial.println(angle5);
Serial.print(«Angle #6: « );
Serial.println(angle6);

set_pos(angle1, angle2, angle3, angle4, angle5, angle6, 50);

}

}

Таким образом, была решена обратная задача кинематики для платформы Стюарта, а также написана управляющая программа для реализации задачи на физической модели с микроконтроллером OpenCM.