Современные мобильные роботы функционируют в заранее неопределенной, изменяющейся среде, взаимодействуют с объектами в ней. В процессе движения робот должен оценивать обстановку: отслеживать собственные координаты, классифицировать окружающие его объекты и определять их положение. Для этого используются различные датчики и системы - для определения координат робота служат: спутниковая навигация, маяки различных принципов действия, колесная одометрия, инерциальные системы и лазерные дальномеры. Окружающие объекты также выделяют с помощью датчиков, измеряющих различные физические величины: радиолокационных и ультразвуковых, тактильных, термометрических, химических, а также широкого круга оптических датчиков от фотореле до лазерных дальномеров и телекамер. Особое место среди оптических локационных систем занимают системы технического зрения (СТЗ). Цифровая телекамера, в отличие от точечного фотореле или датчика цвета, представляет собой двумерный массив из тысяч миниатюрных оптических датчиков, что позволяет получить намного больше сведений об окружающей среде (Рис. 1.1). Сигналы с этого массива преобразуются в яркость и цвет отдельных дискретных элементов – пикселей, образующих цифровое изображение рабочей сцены. В состав СТЗ входят цифровые телекамеры (от одной до нескольких штук), вычислительное устройство и комплекс программных средств для анализа изображения, в частности для выделения на нем интересующих объектов.
 Рис. 1.1. Робот использует СТЗ для получения данных о дорожной разметке
Рис. 1.1. Робот использует СТЗ для получения данных о дорожной разметке
Рост производительности доступных вычислительных средств в последние десятилетия позволяет извлекать из изображений все больше полезной информации. Благодаря этому стало возможным решать с помощью СТЗ все более сложные задачи в режиме реального времени, которые раньше решались с помощью множества других датчиков. Все это позволяет применять такие подходы в том числе и в мобильной робототехнике. Классическим примером использования СТЗ является автоматизированная перевозка грузов на складах или в производственных цехах с помощью «Робокаров» – самодвижущихся транспортных механизмов (Automated Guided Vehicles – AGV), оснащенных системой технического зрения (СТЗ) и оптическим детектором на базе линейки инфракрасных (ИК) датчиков (Рис. 1.2).
 Рис. 1.2. Робокар компании Rocla
Рис. 1.2. Робокар компании Rocla
Одной из ключевых задач СТЗ является распознавание образов, т.е. заданных определенными признаками объектов сцены. Частным случаем распознавания, широко используемым на производстве и в сервис- ной робототехнике, является нахождение в кадре заданных контрастных маркеров или направляющих линий, по которым робокар ориентируется в процессе движения, или других объектов, используемых в качестве
маркеров. В результате, текущее положение робокара определяется на основании данных о положении, размере и ориентации искомого маркера в кадре (Рис. 1.3).
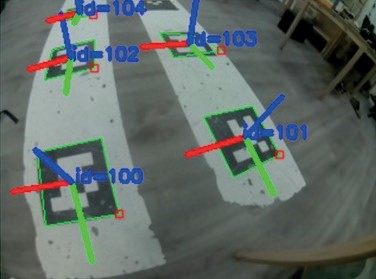 Рис. 1.3. Распознавание специальных маркеров на изображении
Рис. 1.3. Распознавание специальных маркеров на изображении
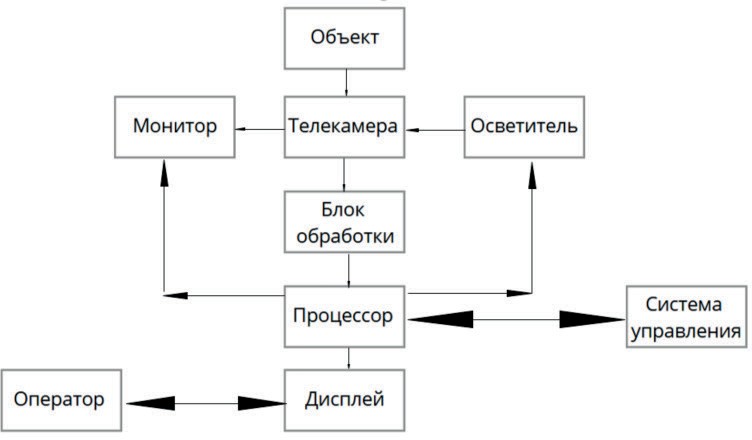 Рис. 1.4. Структура и вид одношинной СТЗ
Рис. 1.4. Структура и вид одношинной СТЗ
Одним из наиболее распространенных решений, используемых при решении задач технического зрения, является однопроцессорная (одношинная) структура СТЗ (Рис. 1.4), построенная на базе персонального компьютера, выступающего в роли вычислительного модуля. В целях уменьшения времени на пересылочные операции из памяти в процессор и обратно, потоки информации разделяют. Т.е. создают многомашинные и многопроцессорные структуры, способные обрабатывать большие потоки видеоданных, поступающих как с одной, так и с нескольких телекамер. Помимо аппаратной части, в СТЗ не менее важной и сложной частью является соответствующее программное обеспечение, необходимое для ввода и обработки визуальных данных. Современные программные средства в этой области можно разделить на 3 группы:
- Инструментальные средства для обращения к аппаратным средствам из приложений (SDK, от англ. «Software development kit»);
- Библиотеки с реализацией алгоритмов обработки изображений;
- Программные пакеты для ввода и обработки зрительных данных в интерактивном режиме.
Инструментальные средства разработки (SDK) для ввода видеоданных – это комплекс программ, предоставляющих приложениям доступ к устройствам ввода («Фреймграбберам») и источникам видеоданных (телекамерам). В настоящее время в робототехнике для обработки изображений получила широкое распространение библиотека OpenCV, со- стоящая из большого количества алгоритмов, поставляемых с документированным API (от англ. «Application programming interface» – интерфейс программирования приложений или интерфейс прикладного программирования) и примерами приложений на языках программирования С/ С++, позволяющих разрабатывать наиболее производительные программы.
Процесс преобразования информации в СТЗ можно представить в виде шести основных этапов:
- Ввод (восприятие) информации, т.е. получение изображения рабочей сцены с помощью датчиков;
- Предварительная обработка изображения с использованием методов подавления шума и удаления графических искажений;
- Сегментация, т. е. выделение на изображении одного или нескольких объектов сцены, представляющих интерес;
- Описание, т.е. определение характерных параметров (цвета, размеров, формы и т.д.) каждого объекта, необходимых для его выделения на сцене;
- Распознавание объекта, т.е. установление его принадлежности к некоторому классу деталей, например, к «Болтам»;
- Интерпретация, т.е. получение искомых величин, в частности, выявления принадлежности объекта к группе распознаваемых, например, «На сцене есть несколько гаек».
В соответствии с тем, какие этапы преобразования информации реализуются в конкретной системе, ее можно отнести к СТЗ высокого, среднего или низкого уровня. Так, задачи, решаемые СТЗ низкого уровня, ограничиваются вводом и предварительной обработкой информации, имея на выходе лишь небольшой набор определенных параметров, например - на сцене обнаружено 5 цветовых областей, из которых 2 красные и 3 синие. Для решения задач образовательной и любительской робототехники таких выдаваемых данных, как правило, бывает достаточно.
Цветовые модели и их восприятие
Говоря о распознавании цветных объектов сцены, необходимо иметь представление искомого цвета в кодировке одной из нескольких цветовых моделей. Цветовая модель – модель описания цветов в виде набора чисел, называемых цветовыми компонентами или цветовыми координатами. Цветовые модели разделяют на три класса:
- Аппаратно-зависимые (описывающие цвет, применительно к конкретному устройству цветовоспроизведения — RGB, CMYK);
- Аппаратно-независимые (для однозначного описания информации о цвете — XYZ, Lab);
- Психологические (основывающиеся на особенностях человеческого восприятия — HSB, HSV).
Например, RGB – аддитивная цветовая модель, цвета которой получаются при смешивании красного, зеленого и синего цветов, как лучей источников цвета (черный цвет получается при нулевых значениях составляющих, а белый – при максимальных). На рис. 1.5 также представлена модель CMYK в виде цветового куба, где чистые цвета образуют его вершины, а оттенки серого лежат на главной диагонали.
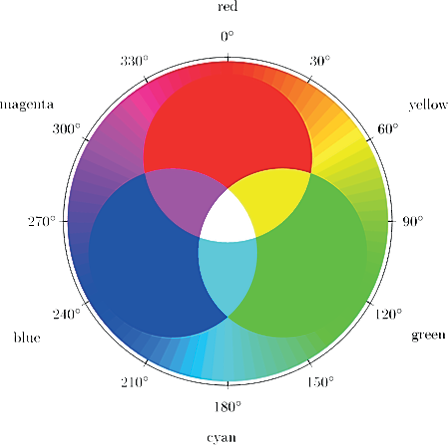
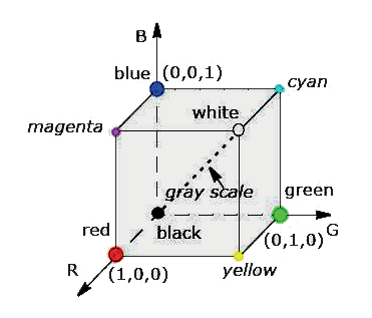
Рис. 1.5. Представление классических цветовых моделей
Модель RGB происходит из особенностей физиологического восприятия цвета сетчаткой человеческого глаза и соответствует физическому принципу как получения изображения в цифровых телекамерах, так и отображения информации на устройствах вывода. Матрица телекамеры/монитора, как правило, состоит из фоточувствительных элементов с фильтрами/индикаторами красного, зеленого и синего цвета. Поэтому изображения в формате RGB используются в СТЗ на этапах ввода-вывода, передачи между приложениями, хранения и, иногда, обработки.
Наибольшее количество задач в СТЗ решается при обработке полутонового изображения в оттенках серого – при этом используется только
яркостная информация. Такой подход позволяет выделять контуры объектов, углы, пятна и, таким образом, определять их форму и положение, что и требуется в большинстве рассматриваемых задач. Это связано с тем, что цветовая информация в большей степени зависит от условий работы и подвержена шуму. Однако, в ряде задач проще пометить известные объекты яркими цветными метками и искать их на изображении, чем анализировать форму этих объектов. По такому принципу цветом кодируются типы объектов и зоны в соревновательных задачах для учащихся школьного возраста. В таких случаях удобно, когда величины, описывающие цвет объекта, не зависят от яркости – цветовые признаки инвариантны к освещенности.
Такое представление цвета реализуется в перцепционных цветовых моделях, основанных на раздельном представлении информации о цвете и яркости.
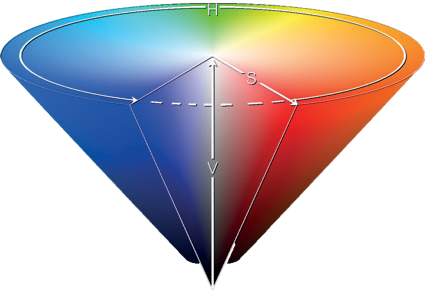
Популярная в графических редакторах перцепционная модель HSV (или близкая к ней HSB), напоминает способ, используемый художниками для получения нужных цветов — смешивание белой, черной и серой красок с чистыми красками для получения различных тонов и оттенков. При этом, цвет задается с помощью трех независимых величин – цветового тона H («Hue»), насыщенности S («Saturation») и светлоты V («Value») или B («Brightness»). В качестве геометрической интерпретации модели HSV используют конус (Рис. 1.6, а), полученный как сглаженная проекция цветового куба в модели RGB вдоль его главной диагонали (Рис. 1.6, б).
Цветовая модель HSV широко используется в интерфейсах настройки СТЗ как интуитивно понятная, а также при обработке изображений для обеспечения инвариантности цвета объекта к его освещенности. Недостатком является вычислительная сложность преобразований, обусловленная замкнутостью шкалы тона H, а также преобразования исходной информации с матрицы в этот формат. Распространенными в передаче изображения в СТЗ цветовыми моделями, в которых яркость выделена в отдельный канал, являются YCbCr и YPbPr.
 a) - цветовой конус
a) - цветовой конус
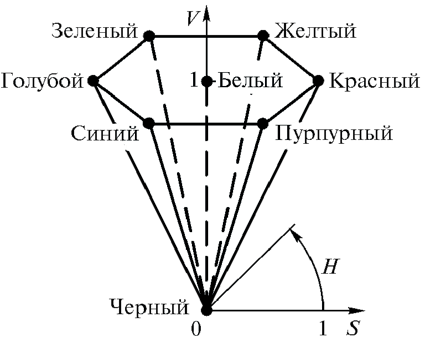 б) - проекция куба RGB
Рис. 1.6. Геометрическая интерпретация цветовой модели HSV:
б) - проекция куба RGB
Рис. 1.6. Геометрическая интерпретация цветовой модели HSV:
В аббревиатуре YCbCr обозначено: Y - компонента яркости, Cb и Cr являются синей и красной цветоразностными компонентами, получаемыми как разность компоненты яркости и соответствующей компоненты цветности.
Составляющие Cb и Cr не являются инвариантными к освещенности и не имеют интуитивно понятного смысла, а модель представляет скорее способ кодирования информации, удобный для сжатия и передачи. Тем не менее, при использовании данной цветовой модели, СТЗ, получая изображение в таком формате, может сразу работать непосредственно с яркостной составляющей Y. А при нормировании цветоразностных компонент Cb и Cr по яркости получается инвариантная к освещенности модель с приемлемым цветовым охватом. Такой принцип реализован в модуле технического зрения TrackingCam.
Наиболее объективную характеристику цвета получают в «аппаратно-независимых» цветовых моделях. Эти модели (к ним относятся модели XYZ и Lab) получили название «Математических». Они строятся на основе хроматической диаграммы, разработанной Международной комиссией по освещению CIE (франц. «Commission internationale de l’éclairage») и основанной на характеристиках среднестатистического глаза человека. Сама диаграмма представляет собой функцию трех переменных Х, Y и Z, описывающих некоторые гипотетические основные цвета. Обычно, модель XYZ используется для измерения способности устройства воспроизвести цвета, с помощью так называемых цветовых охватов – «Гамутов».
Сегментирование как способ распознавания объектов
Следом за СТЗ низкого уровня следуют системы среднего уровня. Для таких систем характерны решения задач сегментации, описания и выделения отдельных объектов на сцене. Причем, описание в данном случае сводится к использованию подходов, основанных на аналитических представлениях – признаки объекта задаются неким математическим условием, к проверке которого и сводится достижение результата распознавания. Рассмотрим два примера такого подхода.
Выделение окружностей
Важной функцией технического зрения является поиск и выделение окружностей на изображении. Такую функцию часто используют для первичного детектирования дорожных знаков и светофоров. В результате работы алгоритмов можно получить значения радиусов и координат центров окружностей, найденных на изображении. Одним из наиболее эффективных на сегодня методов поиска аналитически заданных примитивов является группа методов, основанных на идее преобразования Хафа. Основная идея преобразования Хафа сходна с идеей хорошо знакомого всем по курсу школьной геометрии метода “Общих геометрических мест”. Вспомним, например, задачу построения треугольника по трем его заданным сторонам. Вначале произвольным образом строится одна сторона треугольника (Рис. 1.7):
 Рис. 1.7. Произвольно построенная сторона треугольника
Рис. 1.7. Произвольно построенная сторона треугольника
После этого проводятся две окружности с радиусами, равными длине соответственно второй и третьей сторон треугольника, и центрами, совпадающими с концами первой построенной стороны (Рис. 1.8).
Эти окружности являются “геометрическим местом точек”, где могли бы заканчиваться искомые стороны треугольника. Для всех точек левой окружности выполняется свое условие, для всех точек правой - свое. Точки пересечения двух окружностей являются точками, в которых выполняются оба условия, и, таким образом, это и есть искомая третья вершина треугольника - “общее геометрическое место” (Рис. 1.9).
Обобщая эту методику геометрического построения, можно сказать, что было осуществлено “голосование” в пользу возможного положения вершины. При этом, в голосовании участвовали две точки (концы первого отрезка), и в результате проведения процедуры голосования
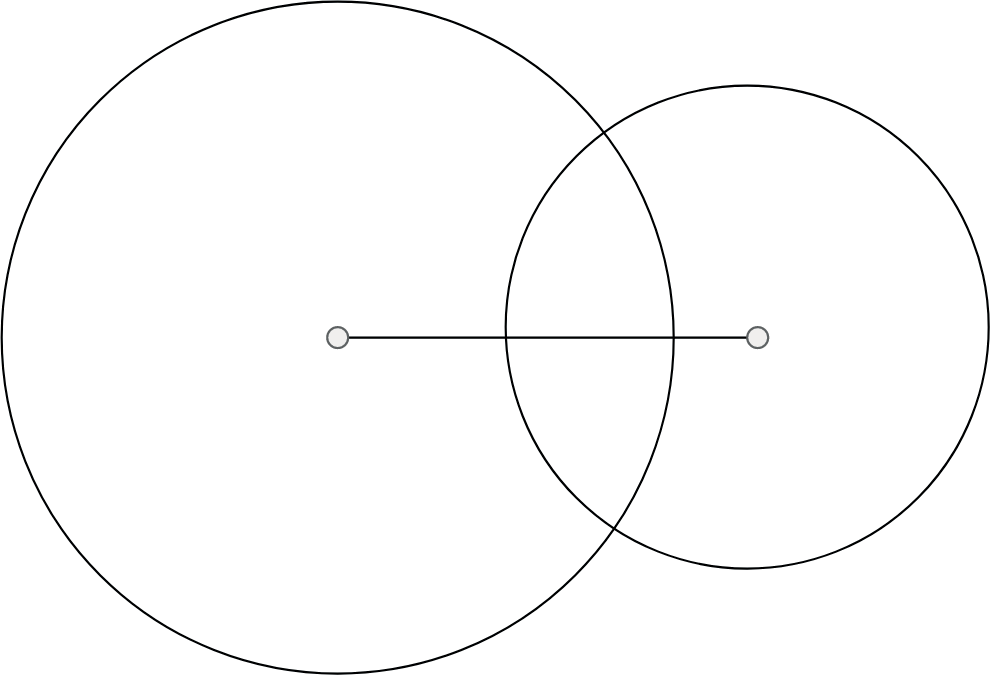 Рис. 1.8. Построение двух окружностей
Рис. 1.8. Построение двух окружностей
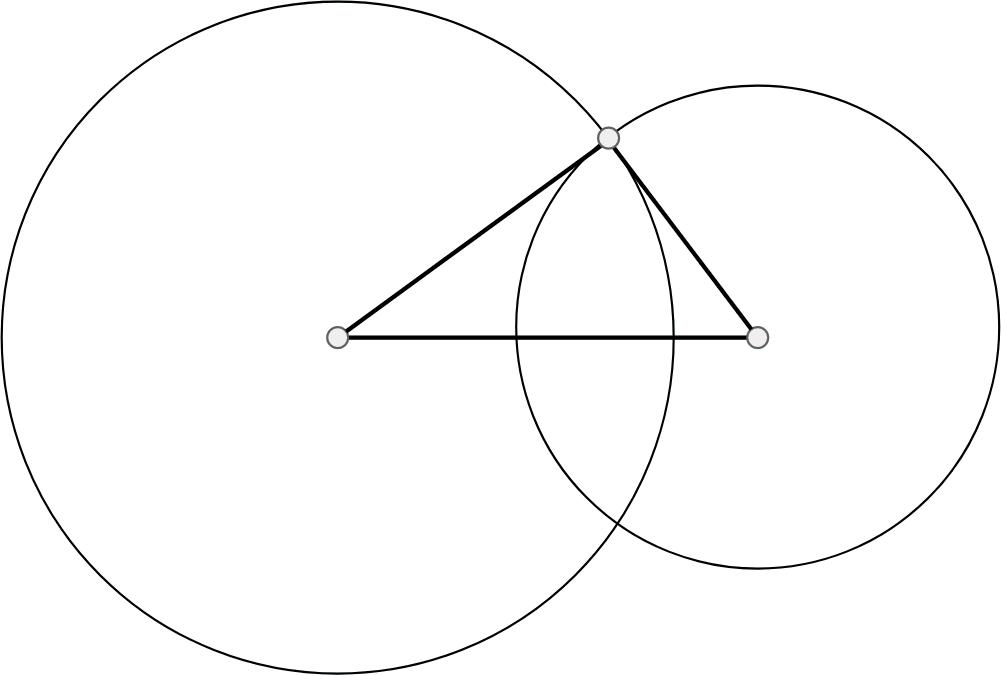 Рис. 1.9. Окончание построения треугольника
Рис. 1.9. Окончание построения треугольника
победила та точка, которая набрала максимум голосов (в данном случае, как видно, два голоса, в отличие от остальных точек плоскости, получивших ноль или один голос). При этом форма “голосующей” кривой для каждой точки определялась нашими знаниями о геометрических характеристиках искомого объекта (в данном случае - заданными длинами сторон треугольника).
Аналогичным образом решается еще одна известная школьная задача - о построении окружности по трем заданным точкам (Рис. 1.10):
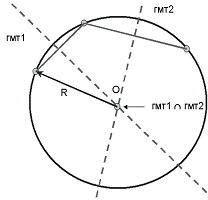 Рис. 1.10. Построение окружности по трем заданным точкам
Рис. 1.10. Построение окружности по трем заданным точкам
В этом случае в качестве общих геометрических мест выступают серединные перпендикуляры к отрезкам, попарно соединяющим заданные точки.
Рассмотрим теперь, как эта идея может быть модифицирована для работы с реальными данными на изображениях, когда требуется найти тот или иной геометрический примитив, за- данный аналитическим уравнением, и при этом, на изображении имеется не две и не три, а значительное количество голосующих точек. На рис. 1.11 показано решение задачи обнаружения окружности известного радиуса в бинарном точечном множестве, в котором могут присутствовать и «ложные» точки (Рис. 1.11, а). Очевидно, что набор центров всех возможных окружностей радиуса R, проходящих через каждую конкретную точку, образует окружность радиуса R вокруг этой точки. Таким образом, геометрическое место точек, которые могли бы быть центрами окружности данного размера, проходящей через эту точку, представляет собой окружность такого же размера с центром в голосующей точке. Наилучшее решение относительно положения центра «наиболее вероятной» присутствующей в данном точечном множестве окружности соответствует точке пересечения максимального числа голосующих окружностей (на Рис. 1.11, б). Точка - «Победитель голосования» помечена большим кружком, а соответствующая ей окружность сплошным контуром).
Таким образом, метод голосования действительно позволяет решать и «некорректные» с точки зрения школьной геометрии задачи анализа избыточных и противоречивых пространственных данных.
А что случится, если на изображении присутствует несколько фигур заданной формы (в рассматриваемом примере - несколько окружностей заданного радиуса)? Тогда у нас возникнет несколько кандидатов с достаточно большим количеством поданных голосов. Если в нашу задачу входит поиск и обнаружение всех таких объектов, то решение задачи будет представлять собой список из нескольких «Победителей голосования», в чью пользу было подано достаточное количество голосов, чтобы они преодолели установленный барьер минимального «избирательного ценза» (порог на количество поданных голосов).
Опишем теперь алгоритм обнаружения окружностей заданного радиуса на полутоновых изображениях, использующий оценку ориентации нормали в голосующих контурных точках. Первым шагом процесса является обнаружение пикселей края, окружающих периметр объекта.
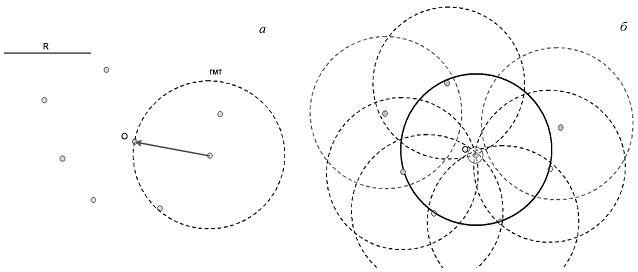 Рис. 1.11. Обнаружение окружности известного радиуса в бинарном точечном множестве методом голосования
Рис. 1.11. Обнаружение окружности известного радиуса в бинарном точечном множестве методом голосования
Например, может использоваться оператор Собела, дающий оценку амплитуды и направления вектора-градиента. Голосующими контурными точками считаются точки с высоким значением модуля градиента. Для каждого обнаруженного краевого пиксела используется оценка положения и ориентации контура с целью оценки центра кругового объекта радиуса R путем движения на расстояние R от краевого пиксела в направлении нормали к контуру (то есть в направлении вектора-градиента). Если эту операцию повторять для каждого краевого пиксела, будет найдено множество положений предполагаемых точек центра, которое может быть усреднено для определения точного местонахождения центра (Рис. 1.12).
Таким образом, изложенными выше методами можно выделять окружности на сцене и определять их характеристики.
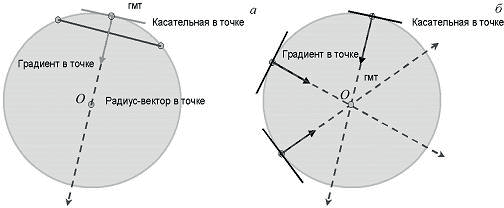 Рис. 1.12. Принцип обнаружения окружности неизвестного радиуса на полутоновом изображении методом голосования
Рис. 1.12. Принцип обнаружения окружности неизвестного радиуса на полутоновом изображении методом голосования
Распознавание Aruco-маркеров
Одной из основных задач СТЗ является локализация объекта или самой камеры относительно некоторого объекта. Существует достаточно много подходов для решения такой задачи, но зачастую, самым простым решением является использование меток, размещенных на объектах. В настоящее время существует достаточно много различного вида меток, доступных для отслеживания – начиная от обычных штрих-кодов, заканчивая QR-метками, способными содержать большое количество информации. Однако, для навигации потенциального робота по меткам, метка должна содержать такое количество информации, чтобы на ее основании можно было выстроить полноценную систему координат, относительно которой можно было бы полноценно рассчитать маршрут. Такими метками стали Aruco-маркеры. Такой маркер представляет собой квадрат с ярко выраженными границами, внутри которого располагается множество белых узоров, которые позволяют однозначно идентифицировать его (Рис. 1.13).
 Рис. 1.13. Пример внешнего вида Aruco-маркеров
Рис. 1.13. Пример внешнего вида Aruco-маркеров
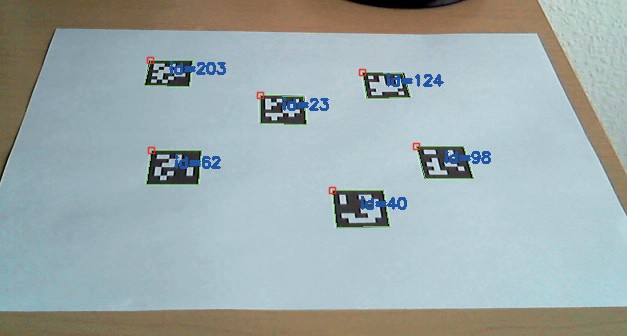 Рис. 1.14. Результат распознавания ID маркеров Aruco
Рис. 1.14. Результат распознавания ID маркеров Aruco
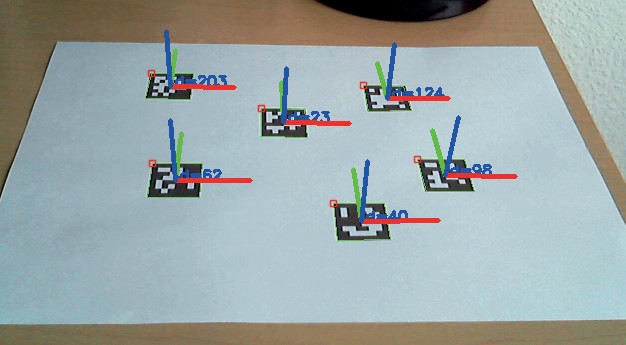 Рис. 1.15. Результат распознавания координат маркера Aruco
Рис. 1.15. Результат распознавания координат маркера Aruco
Теперь, разобравшись в общей концепции работы Aruco-маркеров, следует немного углубиться в процесс определения маркеров. Сами маркеры в системе определяются, как квадратный массив n х n. Общий принцип работы с Aruco маркерами следующий. Aruco-маркеры закрепляют в различных точках на карте. Затем, когда модуль технического зрения видит какой-либо Aruco–маркер, он его фиксирует и распознает с целью получения ID маркера и фиксации его системы координат. После чего происходит определение системы координат маркера относительно базовой системы координат, что, в свою очередь, дает возможность однозначно локализовать местонахождение маркера и определить положение робота относительно маркера.
Процесс распознавания маркера Aruco происходит следующим образом:
- Маркер сегментируется на n^2 количество квадратов (сетку) (Рис. 1.16):
 Рис. 1.16. Сегментирование Aruco-маркера на квадраты
Рис. 1.16. Сегментирование Aruco-маркера на квадраты
- Выделение из маркера квадратов черного и белого цвета (Рис. 1.17):
 Рис. 1.17. Выделение из маркера информации о черном и белом
Рис. 1.17. Выделение из маркера информации о черном и белом
- Получившийся порядок значений маркера сравнивается со значениями известных маркеров, которые известны изначально. Если порядок искомого маркера совпадает с известными, то маркер считается распознанным.
Также стоит отметить, что Aruco-маркер - это, по сути, тот же самый QR-код. Так почему же в робототехнике применяются менее известные Aruco маркеры, а не всеми известные QR-коды? Основное преимущество перед QR-кодами — маркеры Aruco лучше распознаются с дальних дистанций и требуют меньшее количество вычислительной мощи.
В настоящее время подобные маркеры активно используются в робототехнике. Одним из частых решений, в которых используются маркеры Aruco, является задача локализации робота в пространстве (Рис. 1.18). При использовании Aruco-маркеров для локализации робота, следует установить модуль технического зрения и маркеры так, чтобы в процессе движения робота маркеры попадали в область распознавания СТЗ, а так- же правильно выставить освещение.
Плюсы и минусы применения подобных маркеров для локализации робота:
Плюсы:
- хорошая точность, при правильном распознавании;
- небольшие требования к вычислительной мощности;
- не очень сложная реализация;
Минусы:
- во избежание ошибки, необходимо точно установить маркер;
- требуется хороший уровень освещения.
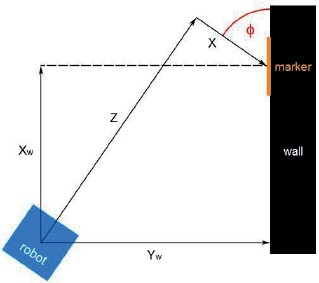 Рис. 1.18. Схематичное изображение процесса локализации робота относительно Aruco маркера
Рис. 1.18. Схематичное изображение процесса локализации робота относительно Aruco маркера
Применение нейросетей
Следующим уровнем развития СТЗ является интегрирование в вычислительный модуль СТЗ алгоритмов, основанных на нейронных сетях. Такие СТЗ уже относятся к СТЗ высокого уровня и позволяют решатьv«следящие» проблемы за счет возможности выделения существенной информации из множества независимых признаков; способности к обучению на примерах и обобщению этих знаний с целью их применения в новых ситуациях; возможности восстановления событий по неполной информации; способности определять цели и формулировать планы для достижения этих целей.
Все эти описанные выше возможности могут быть достигнуты за счет применения нейронной сети YOLO. В модуле технического зрения TrackingCam v3 встроена нейросеть архитектуры YOLO v4 tiny, представляющая собой многослойную сверточную нейронную сеть для решения задачи обнаружения объектов с наилучшим быстродействием. Модели семейства YOLO действительно быстрые, намного быстрее R-CNN и дру- гих архитектур, что позволяет распознавать объекты в реальном времени.
YOLO смотрит на изображение один раз, все изображение разбивается с помощью сетки на ячейки размером S*S. Каждая ячейка отвечает за предсказание нескольких содержащих рамок и вероятности того, что данная рамка содержит объект. Также каждая ячейка отвечает за предсказание вероятностей классов. Таким образом, если ячейка сети предсказывает автомобиль, это не значит, что он там есть, но это значит, что если там есть какой-то объект, то это автомобиль.
Модель YOLO Tiny имеет 9 сверточных слоя и 3 полносвязных слоя. За счет меньшего количества параметров нейросети сокращается количество используемой памяти GPU, что дает возможность использовать алгоритм на встраиваемых системах (Рис. 1.19). Изображение размера 448×448 пикселей пропускается через часть модифицированной модели классификации изображений. В случае несоответствия размера изображения оно будет растянуто под соответствующее разрешение.
Алгоритм работы сети следующий:
На выходе нейросеть дает тензор, размера 7×7×30, который содержит всю информацию, необходимую для нанесения на изображение обрамляющих окон.
- На изображение наносится сетка 7×7. Если центр объекта попадает в ячейку сетки, эта ячейка сетки отвечает за обнаружение этого объекта.
-
Каждой клетке этой сетки соответствует вектор размера (4 + 1) × B
-
C, где:
-
каждое обрамляющее окно (bbox — bounding box) характеризуется пятью показателями:
- (x, y) — координаты центра соответствующей ячейки сетки;
- w — ширина обрамляющего окна, относительно всего изображе- ния;
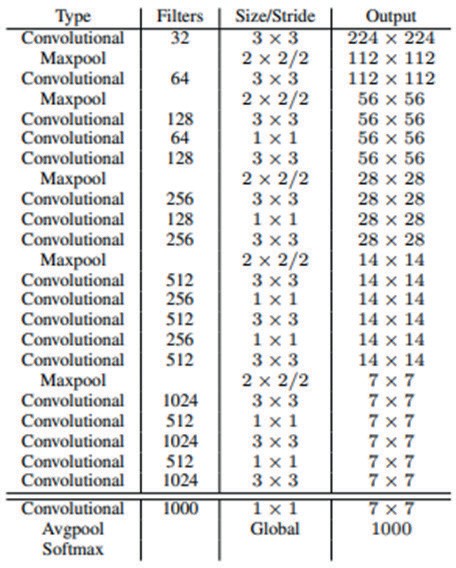 Рис. 1.19. Архитектура YOLO Tiny
Рис. 1.19. Архитектура YOLO Tiny
- h — высота обрамляющего окна, относительно всего изображения.
- некоторая вероятность того, что окно правильно нашло объект: P r(object) * IoUtruth predicted
Здесь ground-truth bboxes — размеченные вручную обрамляющие окна тестирующего набора данных, predicted bounding boxes — предсказанные моделью окна;
- B — число обрамляющих окон для каждой ячейки сетки, B = 2;
- C — число классов, которые могут быть предсказаны.
В каждом из этих элементов вектора хранятся вероятности того, что внутри ячейки сетки лежит объект конкретного класса, без привязки к конкретному оформляющему окну.
- Таким образом, каждая ячейка сетки предсказывает B ограничивающих окон и доверительные оценки (confidence scores) для них.
- Для финального нанесения на изображение обрамляющих окон с полученным набором производятся следующие действия:
- рассматриваются значения набора векторов по классам;
- обнуляются не удовлетворяющие пороговому значению значения;
- сортируются по убыванию;
- на изображение наносятся только те окна, в векторе которых есть ненулевые значения, при этом окну присваивается класс с наибольшим значением.
Ниже на Рис. 1.20 приведен результат работы нейросети YOLO Tiny.
 Рис. 1.20. Пример работы нейросети YOLO Tiny
Рис. 1.20. Пример работы нейросети YOLO Tiny
Center-nav