Глава 4. Практическая часть

В качестве базового объекта управления, входящего в состав образовательного комплекта «СТЕМ Мастерская», выступает манипулятор с плоско-параллельной кинематикой, комплектующие для сборки которого входят в состав набора (инструкция по сборке находится в наборе).

Подготовка к сборке манипулятора

Прежде чем приступать к сборке манипулятора, необходимо предварительно подготовить сервоприводы. Для этого нужно взять 5 сервоприводов с последовательными ID, например, с ID от 1 до 5 (если такие имеются и пронумерованы). Если ID сервоприводов не пронумерованы, можно вручную задать им удобные номера ID. Для этого нужно воспользоваться программным обеспечением RoboPlus и, в частности, рассмотренной ранее программой Dynamixel Wizard 2.0. Процесс переназначения ID сервопривода будет рассмотрен в этой главе далее.

Оборудование, которое понадобится для работы: а. Сервоприводы (рис. 4.1).

Рис. 4.1. Сервоприводы

б. Преобразователь питания DXL-PWR (рис. 4.2)

Рис. 4.2. Преобразователь питания DXL-PWR

в. Преобразователь интерфейса. Данный адаптер используется для преобразования интерфейса Dynamixel в UART компьютера (рис. 4.3)

Рис. 4.3. Преобразователь интерфейса USB-DXL-AR

г. Соединительные кабели (рис. 4.4)

Рис. 4.4. Соединительные кабели

д. Блок питания (рис. 4.5)

Рис. 4.5. Блок питания

е. Программное обеспечение (Dynamixel Wizard 2.0) (рис. 4.6)

Рис. 4.6. Программное обеспечение

Последовательность действий для назначения вручную ID сервоприводов, используя программное обеспечение Dynamixel Wizard 2.0:

Каждый отдельный сервопривод, номер ID которого необходимо переназначить, нужно соединить с преобразователем питания DXL-PWR. Рекомендуется подключать сервопривода по очереди для корректного обнаружения устройств. К нему, в свою очередь, также нужно подключить преобразователь интерфейса Dynamixel
UART (в данном примере будет использоваться модуль USB-DXL- AR). Для подключения устройств между собой воспользуйтесь двумя соединительными кабелями с 3-х пиновыми DXL-разъемами, как показано на изображении 4.7.

Рис. 4.7. Схема подключения сервопривода к преобразователю интерфейса

Рис. 4.8. Программное обеспечение

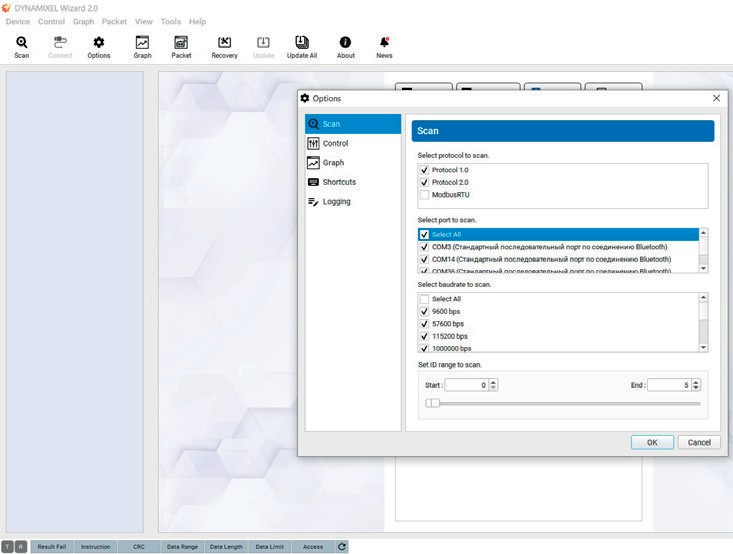
Рис. 4.9. Окно поиска подключенных сервоприводов

Подключите блок питания к преобразователю питания DXL- PWR и к сети 220В, чтобы обеспечить данную цепочку устройств необходимым ей питанием.
Подсоедините преобразователь интерфейса USB-DXL-AR к USB порту компьютера (не забудьте установить драйвера, скачиваемые с сайта appliedrobotics.ru).
Затем запустите программное обеспечение Dynamixel Wizard 2.0 (рис. 4.8).
В левом углу окна открывшейся программы выберите кнопку «Options». (Рис. 4.9).
В открывшимся окне установите необходимый протокол для поиска устройств (2.0), выберите COM порт, к которому в данный момент подключен преобразователь интерфейса USB-DXL-AR, и установите скорость обмена данными (1000000). Нажмите кнопку ОК. (Рис 4.10).

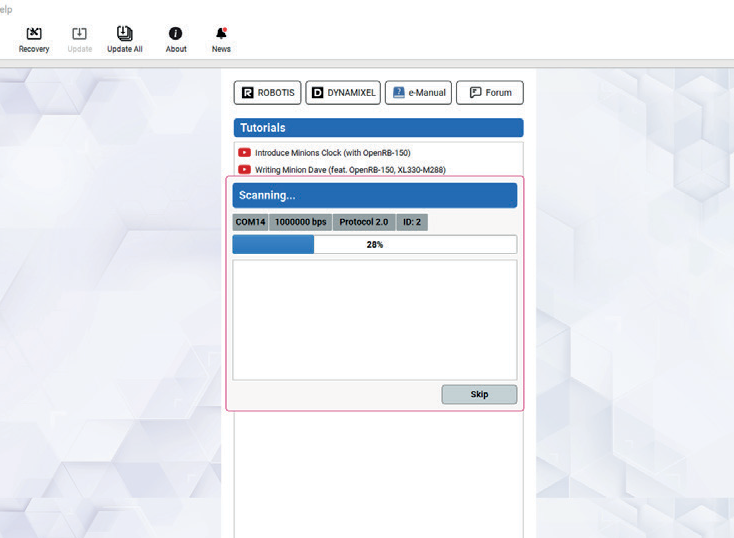
Рис. 4.10. Процесс поиска подключенных сервоприводов

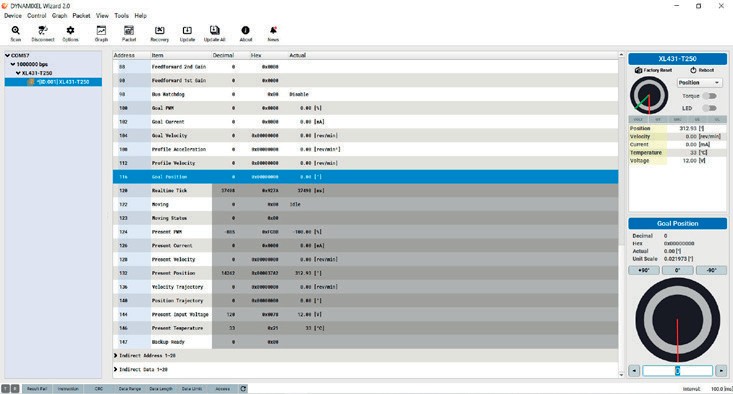
Рис. 4.11. Окно с параметрами выбранного сервопривода

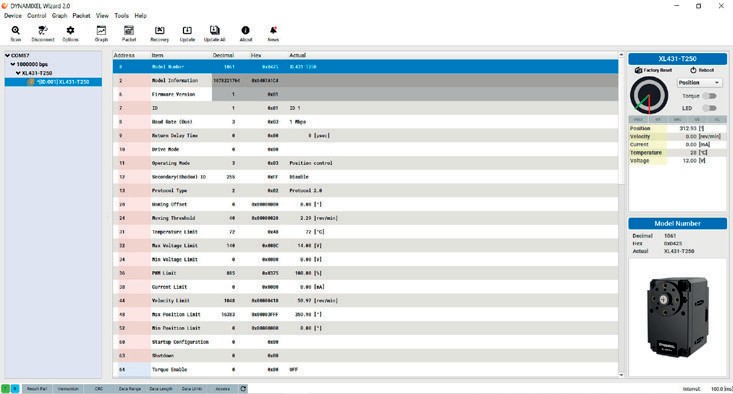
Рис. 4.12. Параметр для управления положением сервопривода

Нажмите кнопку «Scan».
После осуществления поиска устройств в левой части окна будет отображен найденный сервопривод. Следует обратить внимание, что в данную цепочку можно подключать несколько сервоприводов последовательно (например, как они будут подключены на манипуляторе), поскольку в каждом сервоприводе имеется по два 3-х пиновых DXL-разъема, и соединительный кабель можно протянуть от одного сервопривода к другому и т.д. Но в текущем примере на данный момент в окне должен быть отображен всего один сервопривод с некоторым номером ID (в примере – с ID) (рис. 4.11).
Если в отображенном слева списке подключенных устройств выбрать найденный сервопривод, то откроются его параметры (рис. 4.11).
В появившейся таблице параметров выбранного сервопривода нужно изменить значение параметра ID (третья строка). После изменения нажать кнопку Apply. В данной таблице отображаются также и другие параметры сервопривода. Можно протестировать его движение, изменив значение параметра Goal Position в таблице или управляя появившимся справа при выборе параметра ползунком (рис. 4.12).
После окончания работы с сервоприводом необходимо отключить его с помощью кнопки «Disconnect».
После этого можно отключить текущий сервопривод из цепи и заменить его следующим.

Используя вышеописанную инструкцию, нужно по очереди задать ID для всех пяти сервоприводов, используемых при сборке модели манипулятора с плоско-параллельной кинематикой (рис. 4.13).

После успешного выполнения подготовки можно приступать к сборке модели манипулятора.

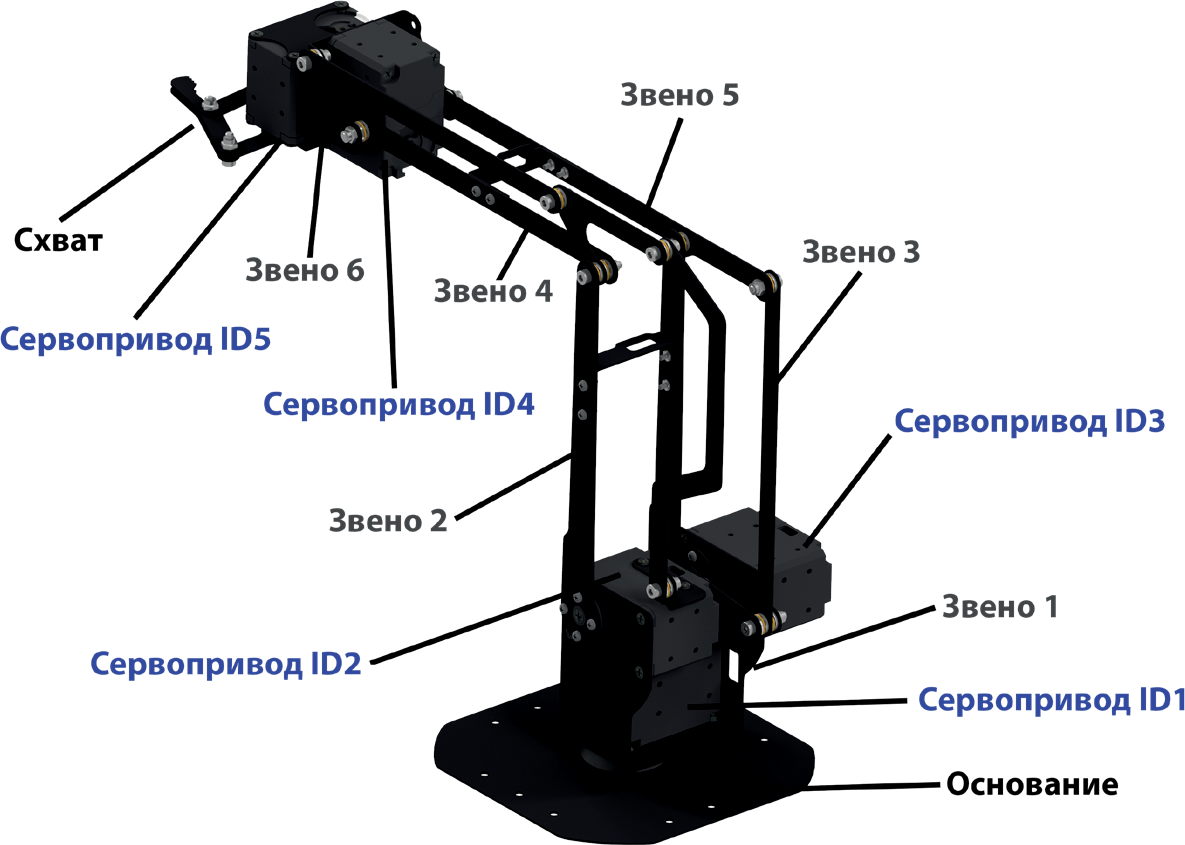
Рис. 4.13. Схема модели манипулятора

Сборка манипулятора

Сборка манипулятора проводится по инструкции, приведенной в приложении. Следует обратить внимание, что нумерация приводов при сборке приведена на рисунке 4.13.

Главное, на что необходимо обратить внимание, это:

Совмещенность одинарных рисок на корпусе и выходном валу сервоприводов. Если риски не будут совмещены, то придется проводить пересборку на этапе программирования, так как манипулятор не сможет корректно отрабатывать некоторые действия и команды (рис. 4.14).

ПРАВИЛЬНОЕ

положение фланца

НЕПРАВИЛЬНОЕ

положение фланца

НЕПРАВИЛЬНОЕ

положение фланца

Рис. 4.14.

Для крепления конструкции к отверстиям в выходном валу сервоприводов ОБЯЗАТЕЛЬНО необходимо использовать винты такой длины, чтобы винты не проходили насквозь отверстий в выходных валах. Так как, в противном случае, винт, пройдя насквозь, может повредить корпус и привести к заклиниванию выходного вала. Что также может привести к поломке сервопривода. Поэтому очень важно при сборке обращать внимание на длину используемых винтов.

По окончанию сборки от самого первого сервопривода должен идти соединительный кабель, который позже будет подключен к плате управления.

Подробнее информация по сборке модели манипулятора с плоскопараллельной кинематикой представлена в отдельном руководстве

«Инструкция по сборке».

Расчеты

Максимальная масса груза

После проектирования элементов конструкции и осуществления сборки манипулятора, прежде всего, желательно дать учащимся понимание основных расчетов манипулятора. Одним из основных шагов расчета манипулятора является выбор используемых двигателей. Подбор двигателей происходит по их мощности и необходимым желаемым техническим характеристикам, которым должен удовлетворять разрабатываемый манипулятор. При разработке данного манипулятора будут применяться сервоприводы. Поэтому, вместо данного шага, зная длины элементов будущей конструкции, а также максимальный момент, который может потянуть сервопривод, вполне возможно сделать расчет максимальной массы нагрузки, которую сможет поднять такой манипулятор. Дальнейшие выкладки приведены из расчета на то, что учащиеся по школьной программе уже знают, что такое момент силы, и как его находить.

В документации на сервоприводы можно найти, что максимальный момент, при котором сервоприводы способны к плавному и точному перемещению нагрузки – 0,3 Н∙м, а максимальный момент, который могут удерживать приводы – 1,5 Н∙м.

Рассчитаем массу полезной нагрузки, например, для 3-го сервопривода, так как из всех сервоприводов манипулятора он самый нагруженный. Ему, помимо массы груза, также требуется перемещать массу всей конструкции манипулятора, которая расположена после – то есть 4 звеньев, схвата, 4 и 5 приводов. Проведем расчет для самой нагруженной конфигурации манипулятора для 3-го привода в момент, когда он выпрямлен, и вся конструкция, начиная с точки соединения 2 – 3 и 4 – 5 звеньев, находится в горизонтальном положении (то есть имеет прямой угол) (рис. 4.15):

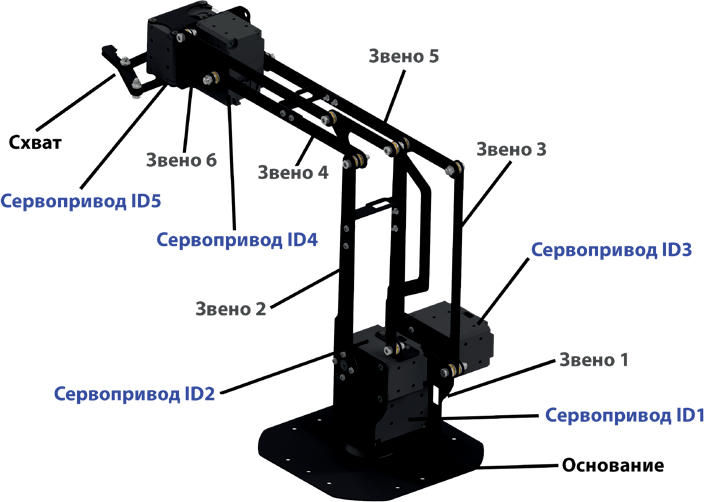
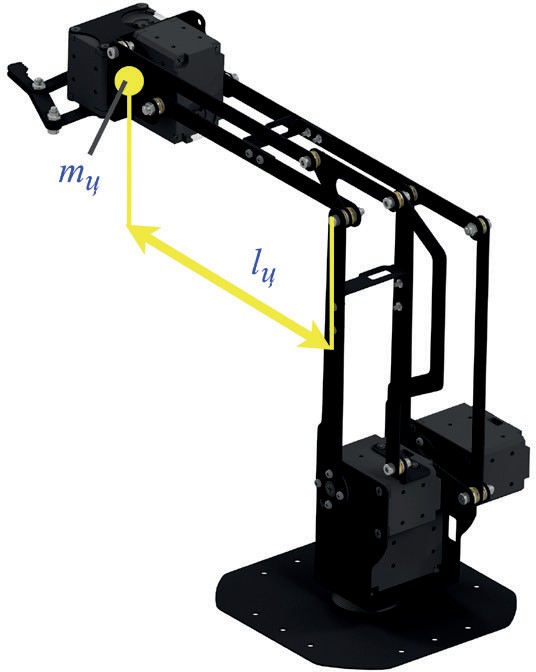
Рис. 4.15. Положение манипулятора при максимальной нагрузке

В этом случае, момент нагрузки на третий сервопривод можно найти по упрощенной формуле:

\(Мнагрузки = g *(mц*lц) + Мгруза\)

где mц=0,25 г – это масса удерживаемой третьим сервоприводом конструкции, а lц=0,21 м – расстояние до центра масс.

Значит, максимальный момент, с которым может справиться данный

манипулятор с плоско-параллельной кинематикой с учетом собственной конструкции, можно вычислить, приняв Mнагрузки максимальным для сервопривода – 1,5 Н∙м.

\(Мгруза=Мнагрузки- g *(mц*lц)\)

\(Мгруза=1,5Н∙м-9,8м*0,0525кг*∙*м/с2=0,9855Н∙м*\)

Учитывая, что плечо груза можно принять равной длине манипулятора в выпрямленной конфигурации от 2 привода до краев захвата, то плечо груза lгруза=0,3 м.

А значит, максимальная масса груза, который может поднять манипулятор, равна \(mгруза=Mгруза/g∙lгруза =0,335кг.\) Однако, нормальное оперирование таким грузом будет невозможно.

Реально сервопривод может уверенно работать с грузами массой в 5 раз меньше, то есть максимально допустимая масса груза m(груза.доп)=0,067кг.

Прямая и обратная задачи кинематики

Помимо расчетов максимальной массы груза, рассмотрим прямую и обратную задачи кинематики (ПЗК и ОЗК, соответственно). Усвоение данных тем потребует от учащихся хорошего знания геометрии, а также освоения основ тригонометрии.

Цель данного этапа – дать учащимся понимание об ОЗК и ПЗК, а также примерное представление о решении этих задач.

Для общего развития: стандартной единицей измерения угла в системе СИ является радиан. Угол 180° – это π≈3,14 радиан. Остальные соответствия можно найти из пропорции. Например 90° – это π/2≈1,57 радиан. Большинство калькуляторов считают именно в радианах.

В первую очередь, необходимо разобрать с учащимися основы тригонометрии, а именно – понятие простых тригонометрических функций. Проще всего это сделать на примере треугольника с прямым углом (рис. 4.16).

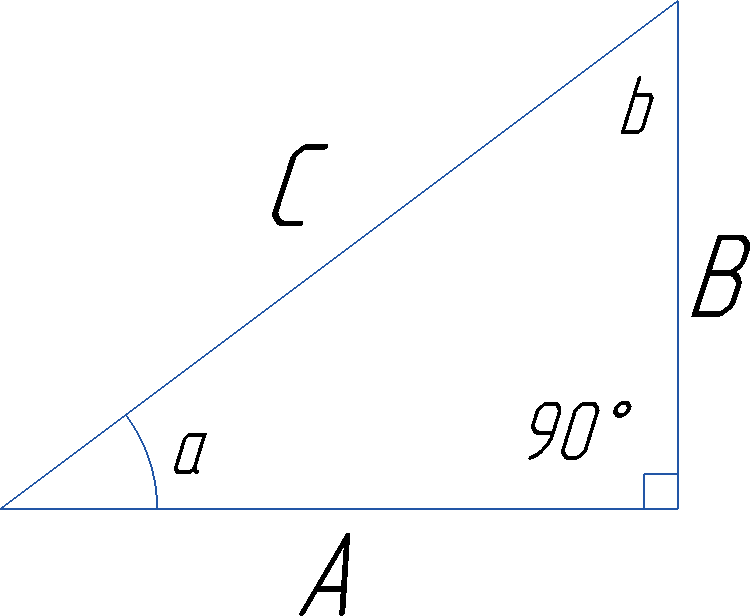
Рис. 4.16. Прямоугольный треугольник

В целом, тригонометрия и тригонометрические функции необходимы для поиска углов и точек в прикладных задачах. Например, в дальнейшем, чтобы управлять манипулятором, необходимо будет задавать углы поворота сервоприводов, рассчитать которые можно из решения ОЗК, которая основывается на тригонометрии.

Итак, есть прямоугольный треугольник с катетами A и B, гипотенузой C и углами α(a), β(b) и 90°. Вопрос – как найти его углы? Конечно, можно воспользоваться транспортиром. Однако транспортир не всегда есть под рукой, да и точность такого измерения не слишком высока. Поэтому, были введены специальные функции, задающие зависимость углов прямоугольного треугольника от сторон (и наоборот), так как при изменении длин сторон неизбежно меняются и углы (и наоборот). Это простейшие тригонометрические функции – синус, косинус и тангенс. Задаются они следующим образом:

Для α:

*\(sin(α)=B/C\)– отношение длины противолежащего катета к длине гипотенузы.

\(cos(α)=A/C\) – отношение длины прилежащего катета к длине гипотенузы.

\(tg(α)=B/A\) – отношение длины противолежащего катета к длине прилежащего катета.

Для β:

\(sin(β)=A/C\) – отношение длины противолежащего катета к длине гипотенузы.

\(cos(β)=B/C\) – отношение длины прилежащего катета к длине гипотенузы.

\(tg(β)=A/B\) – отношение длины противолежащего катета к длине прилежащего катета.

Благодаря использованию данных тригонометрических функций, возможно определить одну из сторон треугольника, зная его угол и вторую сторону. Но если известны именно стороны, и нужно вычислить углы треугольника, можно применить тригонометрические функции, обратные вышеуказанным. Их названия с приставкой «arc» – аркосинус, арксинус, арктангенс и т.д. Они также есть в большинстве современных калькуляторов. Рассчитав соотношение длин сторон и выбрав функцию арксинус (аркосинус, арктангенс), можно вычислить значение угла в радианах, а затем перевести его в градусы.

При наличии транспортира под рукой, можно поэкспериментировать в следующем коротком примере. Начертим прямоугольный треугольник размером 3х4х5см (рис.4.17):

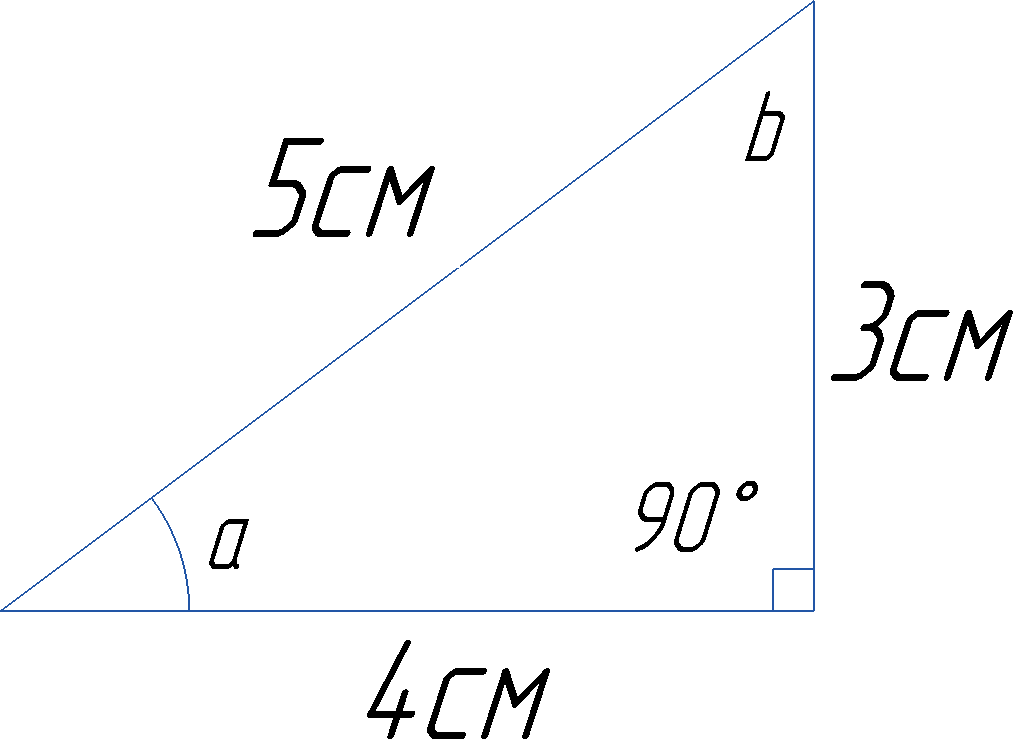
Рис. 4.17. Прямоугольный треугольник со сторонами 3х4х5см

Найдем угол α. Если синус угла α – это отношение противолежащего катета к гипотенузе, то сам угол – это арксинус этого отношения.

\(α=arcsin(3/5)=0,644рад = 36,87°\)

Учитывая, что рассматриваемый треугольник прямоугольный (второй угол треугольника равен 90° ), теперь можно рассчитать угол β.

\(β=180°-90°-36,87°=53,13°\)

Другим способом определения угла β является применение тригонометрической функции arccos, по аналогии с расчетом значения угла α (только в этом случае будет браться отношение прилежащего катета к гипотенузе):

\(β=arccos(3/5)=0,927рад=53,13°\)

Воспользовавшись транспортиром для проверки расчетов, можно получить те же результаты.

Закрепив знания об основных тригонометрических функциях, разберем, что же такое прямая и обратная задачи кинематики, и зачем они нужны.

Прямая задача кинематики

Прямая задача кинематики заключается в следующем:

Допустим, у нас есть манипулятор, и все приводы в нем развернуты на какие-то фиксированные углы. Как же узнать, где находится выходное звено орган управления (в нашем случае, схват), относительно основания манипулятора. Измерять каждый раз расстояние от основания манипулятора до его схвата линейкой не вариант – это долго, очень низкая точность, а иногда такая возможность даже отсутствует. А если манипулятор большой – никакой линейки не хватит. А если манипулятор работает на опасном производстве – то такие измерения и не кому провести. На этот случай и нужна прямая задача кинематики. Она позволяет вычислить математически, где находится рабочий орган манипулятора, зная лишь длины звеньев, а также углы поворота этих звеньев (углы поворота приводов, соединяющих звенья).

Прямая задача кинематики всегда имеет единственное решение (в отличие от обратной, как мы дальше убедимся). И решать ее намного проще, чем обратную. В качестве примера можно рассмотреть конструкцию, состоящую из 2-х сервоприводов и 2-х звеньев, способную к движению на плоскости. Такая конструкция условно представлена на рисунке 4.18:

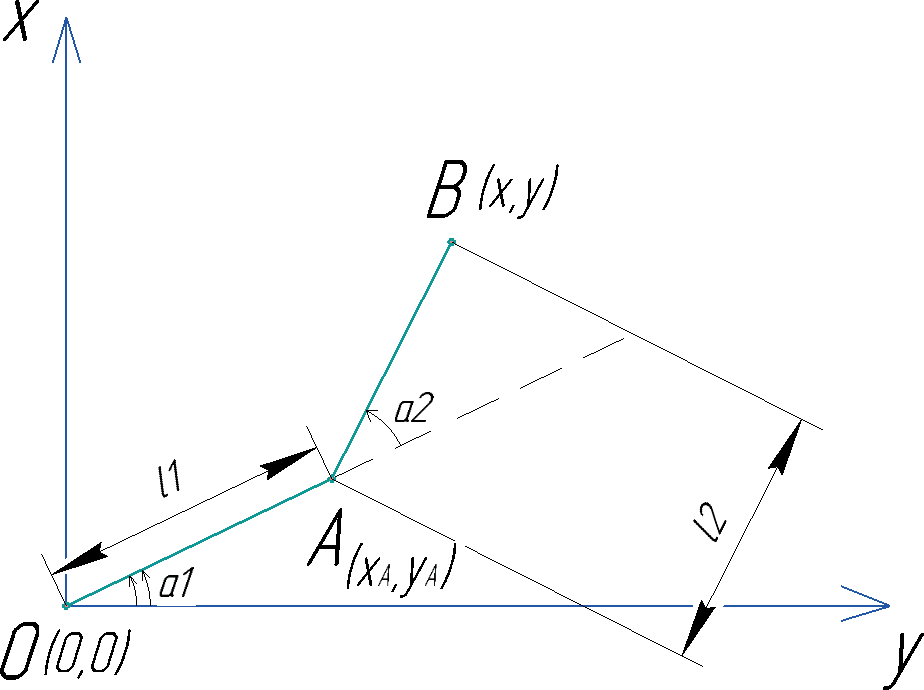
Рис. 4.18. Иллюстрация прямой задачи

Обратив внимание на рисунок, мы увидим, что имеется 2 звена манипулятора, условно представленных отрезками ОА и АВ, и 2 шарнира, расположенных в точках О и А. Длины звеньев l1, l2 и углы их поворота α1,α2

(относительные углы поворота сервоприводов) известны. Для решения

задачи (определения расположения рабочего органа манипулятора) при такой конфигурации манипулятора требуется найти координаты точки B (x, y).

Для нахождения координаты точки B нам потребуется последовательно решить ПЗК. Это значит, что мы по очереди будем искать координаты всех сервоприводов в относительной системе координат, а затем сложим результаты. Сначала найдем координаты точки А (Xa;Ya):

\(хА=l1∙cos(α1)\)

\(yA=l1∙sin(α1)\)

А теперь представим, что исходная система координат находится не в точке О, а в точке А (обозначена X’АY’) (рис. 4.19):

Рис. 4.19. Иллюстрация прямой задачи

В системе координат X’АY’, расположенной в точке А, можно аналогичным образом найти координаты точки В (то есть ищутся координаты точки В относительно точки А):

\(*xBA=l2∙cos(α1+α2) yBA=l2∙sin(α1+α2)*\)

Мы знаем координаты точки А (в глобальной системе координат XOY)

и рассчитали координаты точки В относительно точки А (в вспомогательной системе координат X’AY’). Значит, мы можем вычислить глобальные координаты точки В в системе координат XOY. Для этого необходимо просто сложить соответствующие составляющие по осям X и Y:

\(x=xA+xBA= l1∙cos(α1)+ l2∙cos(α1+α2) y=yA+yBA= l1∙sin(α1)+ l2∙sin(α1+α2)\)

Рассчитав таким образом глобальные координаты точки B (x,y), мы

определим расположение рабочего органа манипулятора в глобальной системе координат. Прямая задача кинематики решена. Очевидно, что при ее решении не приходится сталкиваться со слишком сложными аналитическими и математическими вопросами. И если задача представлена только на плоскости, то при увеличении количества звеньев манипулятора будет просто возрастать количество слагаемых в формулах расчета координат схвата манипулятора.

Для проверки можно также провести математическое решение этой задачи, воспользовавшись транспортиром и линейкой, и убедиться, что представленные выше формулы верны. Однако, при этом важно обращать внимание на следующее: углы α1 и α2 могут быть как положительyыми, так и отрицательными. В качестве положительного направления откладывания углов принимается направление против часовой стрелки. В нашем примере углы α__1 и α__2 положительны.

Обратная задача кинематики

Смысл обратной задачи кинематики противоположен прямой задаче. Допустим, мы знаем, где лежит объект, который должен схватить манипулятор, либо где находится целевое положение рабочего органа, при котором необходимо проводить сварку или пайку. Вопрос в том, как для выполнения этого действия нужно управлять манипулятором? А точнее, как задать углы таким образом, чтобы манипулятор встал в нужное нам положение и поместил рабочий орган именно в ту точку, в которую нам нужно. Поэтому ОЗК противоположна ПЗК – если в ПЗК мы знаем все углы и нам нужно найти положение рабочего органа манипулятора, то в ОЗК целевое положение нам известно, но вот углы поворота приводов, позволяющие обеспечить это положение находятся под вопросом.

Обратная задача кинематики может иметь несколько решений. Рассмотрим это на предыдущем примере. Пусть у нас есть целевая точка B из предыдущего примера с координатами x и y (рис. 4.20).

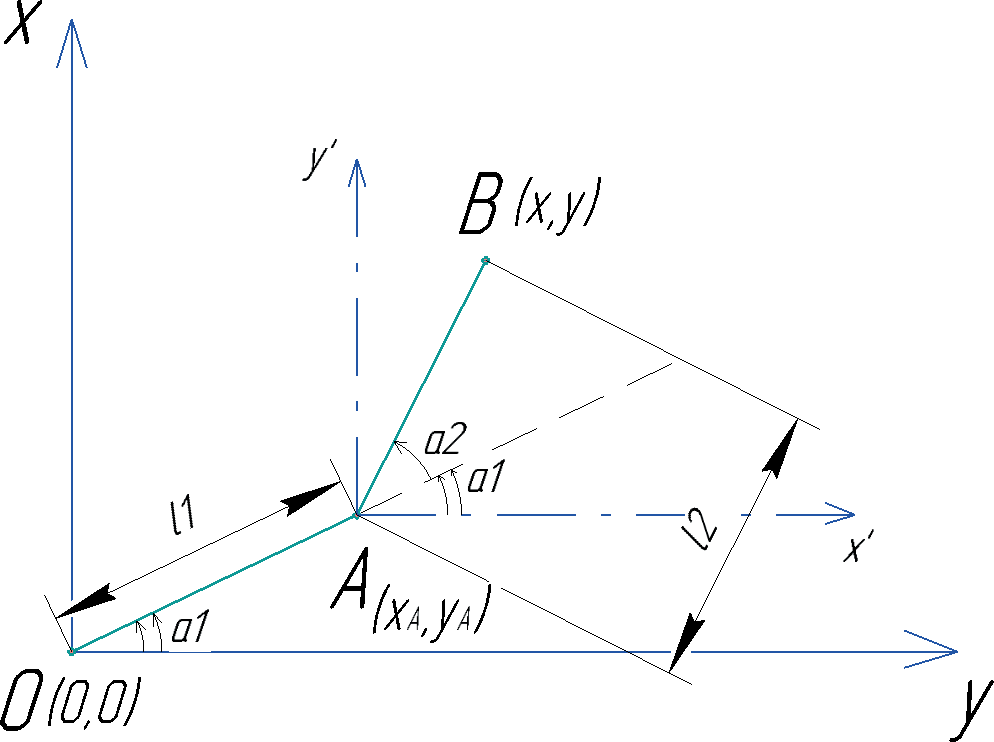
Рис. 4.20. Иллюстрация обратной задачи

На рисунке выше изображено расположение звеньев манипулятора, благодаря которому рабочий орган манипулятора занял свое целевое положение в точке B(x,y). Однако, рабочий орган манипулятора может занять свое целевое положение в точке B(x,y) и по-другому:

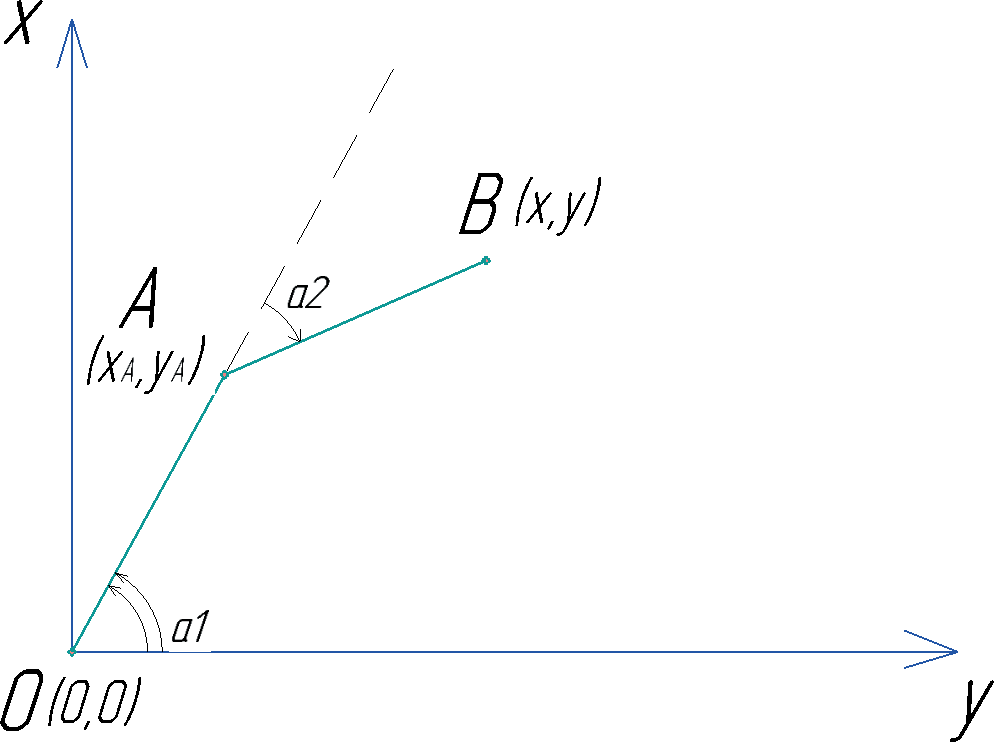
Рис. 4.21. Иллюстрация обратной задачи. Один из вариантов положения звеньев манипулятора в пространстве

Оба варианта расположения звеньев манипулятора возможны. Данный пример наглядно демонстрирует, почему у ОЗК возможно несколько решений.

Рассмотрим решение ОЗК. Проведем дополнительный отрезок d, а также обозначим вспомогательные углы q1 (от оси x до d), q2(от d до OA) и q3(между OA и AB):

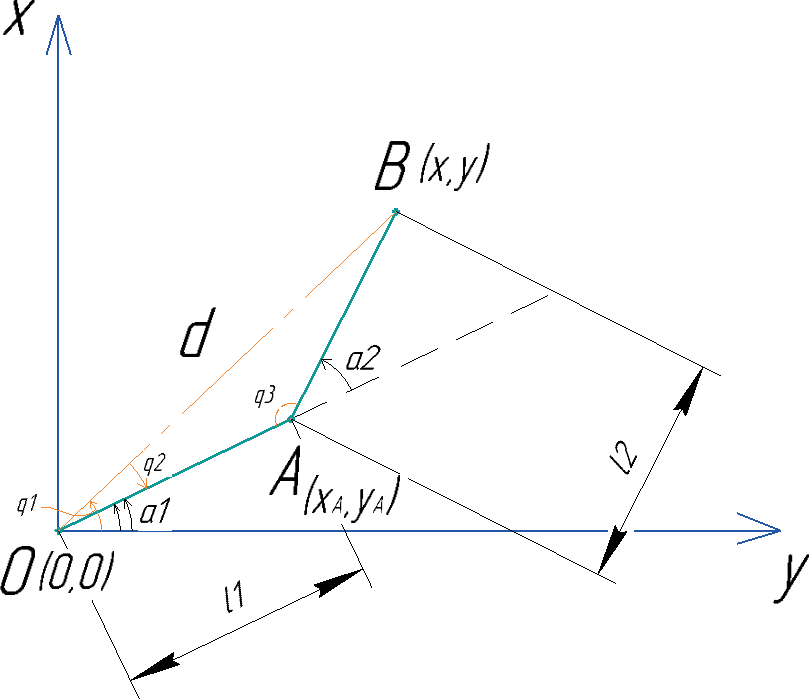
Рис. 4.22. Иллюстрация обратной задачи. Дополнительные построения

По теореме Пифагора:

\(d2=x2+y2 q1=arctg(y/x)\)

\(q2=arccos((d2+l 2-l 2)/2∙B∙l )\)

\(q3=arccos((l 2+l 2-d2)/2∙l ∙l )\)

Таким образом, можно вычислить углы α1 и α2:

\(*α1=q1+q2 α2=π-q3\)*

Следует обратить внимание, что для рассматриваемого случая угол q1 положителен, а q2 отрицателен. Но во втором рассмотренном способе расположения звеньев манипулятора (см. рис. 4.23) углы q1 и q2 положительны. Поэтому сумма q1+q2 будет давать больший α1, чем в текущем случае:

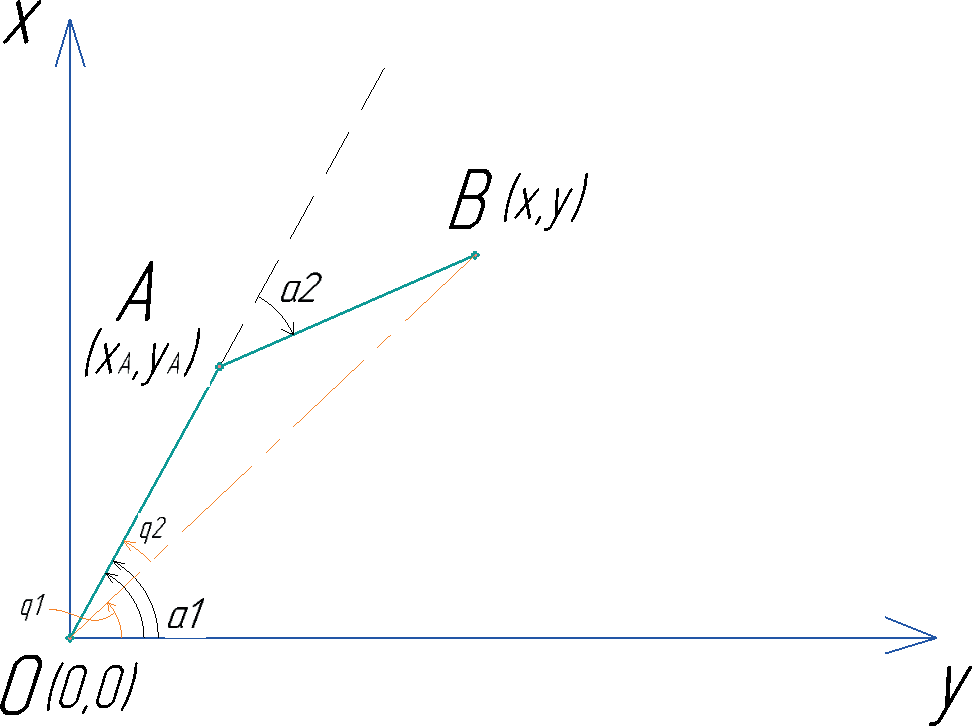
Рис. 4.23. Иллюстрация обратной задачи. Один из двух вариантов расположения звеньев манипулятора в пространстве

Очевидно, что для 2-звенного манипулятора существует всего 2 способа прийти в произвольную точку (2 решения ОЗК). Однако, если манипулятор имеет больше звеньев, число решений ОЗК также увеличивается. Что дополнительно усложняет задачу, так как, зачастую, к решению задачи прибавляется требование по расчету и занятию оптимального положения.