Глава 4. Манипуляторы DIY
Рассмотренные в предыдущей главе модели деталей манипулятора являются составными частями собираемого манипулятора с угловой кинематикой. Таким образом, используя 3D принтер, можно выполнить печать всех необходимых конструктивных элементов углового манипулятора DIY, а затем собрать его. DIY — аббревиатура английского Do It Yourself, то есть — сделай сам.
Угловой манипулятор DIY
Рис. 4.1. Внешний вид манипулятора DIY с угловой кинематикой
Расчеты
Максимальная масса груза
Проведем оценку грузоподъемности робота. В рассматриваемой модели манипулятора применяются сервоприводы DYNAMIXEL XL431- T250-T и сервоприводы AR-S430-01, производимые OOO “Прикладная робототехника”. Их технические характеристики известны. Зная максимальный момент сервопривода, а также длины элементов конструкции модели, можно сделать расчет максимальной массы нагрузки, которую сможет поднять манипулятор.
В документации на сервоприводы можно найти, что максимальный момент, при котором сервоприводы способны к плавному и точному перемещению нагрузки – 0,53 Н∙м, а максимальный момент, который могут удерживать сервоприводы – 1,4 Н∙м.
Используя эти данные, рассчитаем массу полезной нагрузки для 2-го сервопривода в статическом положении, поскольку он является самым нагруженным из всех сервоприводов манипулятора. Первая степень в расчетах не учитывается, так как ось вращения вертикальна. Второму сервоприводу, помимо массы груза, также требуется перемещать массу всей конструкции манипулятора, которая расположена после него – то есть, 5 звеньев и 4 привода. Расчет будем проводить для самой нагруженной конфигурации манипулятора для второго сервопривода – горизонтальном положение, параллельно поверхности (рис. 4.2).
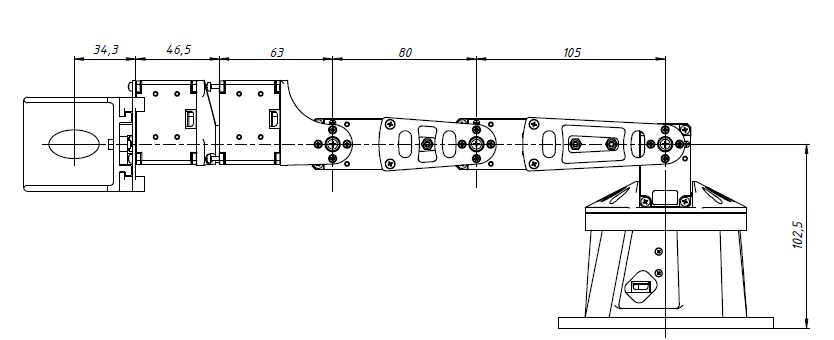
Рис. 4.2. Максимально нагруженное положение манипулятора
Формула для вычисления момента нагрузки на втрое звено имеет вид:
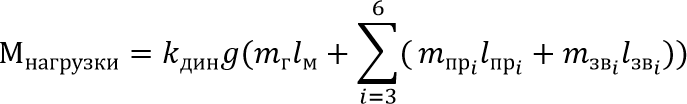
\(K_{дин}\) - коэффициент динамики. Расчет производится для статического положения манипулятора, однако требуется учитывать динамические нагрузки. Стандартное значение \(K_{дин}\) = 1,4.
\(g\) - ускорение свободного падения.
\(m_г\) - масса груза.
\(l_м\) - расстояние до центра масс зацепа груза.
\(m_{пр_i}\) - масса i-го сервопривода.
\(l_{пр_i}\) - расстояние до центра масс i-го сервопривода.
\(m_{зв_i}\) - масса i-го звена манипулятора.
\(l_{зв_i}\) - расстояние до центра масс i-го звена манипулятора.
Примем расстояние до захватываемого груза 328,8 мм – длина от оси вращения второго сочленения до окончания схвата манипулятора.
\(\displaystyle\sum_{i=3}^{6} m_{пр_i}\)= 228 грамм - суммарная масса сервоприводов.
Для упрощения решения задачи будем считать, что центр масс сервопривода располагается в центре вала вращения. Таким образом, найдем плечо до каждого сервопривода от оси вращения второго сочленения (рис. 4.2).
Необходимую массу звеньев и центра масс узнаем с помощью модели в САП.
Масса звеньев робота зависит от формы, используемых материалов и технологии изготовлении. В случае использования стандартной модели звеньев манипулятора суммарная масса:
\(\displaystyle\sum_{i=3}^{6} m_{зв_i}\)=116грамма
Центр масс, учитывающий звенья третьей, четвертой, пятой и шестой степеней свободы, располагается на расстоянии 220 мм от оси вращения второго сервопривода.
Для нахождения массы груза с которым манипулятор имеет возможность взаимодействовать составим уравнение:
Таким образом момент, \(M{нагрузки}\) создаваемый нагрузкой на второе сочленение, равняется моменту сервопривода \(M{серв}\)
Из электромеханической характеристики сервопривода найдем крутящий момент:
Приведем известные значения к системе СИ и подставим в формулу:
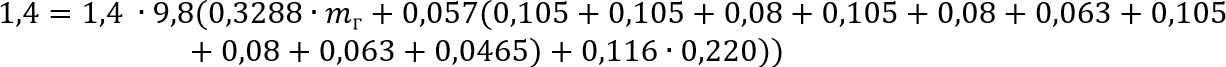
Преобразуем значения:
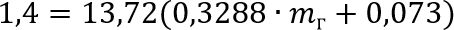
Выразим и найдем массу груза \(m_г\):
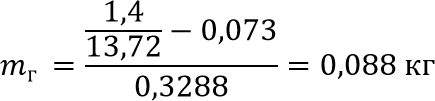
Таким образом, максимальная масса груза для обеспечения нормальной работы манипулятора составляет 88 грамм. Однако, это приблизительный расчет, так как исследовалось статическое и наиболее нагруженное положение манипулятора.
Обратная задачи кинематики
Рассмотрим решение обратной задачи кинематики (ОЗК) для манипулятора с угловой кинематикой. Для исключения избыточных случаев можно принять положение выходного звена манипулятора вертикальным, при этом, захват будет все время находиться в вертикальном положении. В этом случае, ОЗК будет решаться однозначно.
Манипулятор можно условно разделить на 4 линейных сегмента с
соответствующими длинами l1,l2 ,l3 ,l4 . Причем, на первом и четвертом
звеньях находятся сервоприводы, дающие вращательную степень свободы вдоль продольной оси звена (Рис. 4.3).
Зеленым цветом показаны звенья манипулятора. Крестиками отмечены продольные степени вращения.
При данных условиях (звено 1 имеет только продольную степень вращения, расположено вертикально, звено 4 расположено вертикально, а 5-ый сервопривод также дает вертикальную степень вращения) можно абстрагироваться от всех звеньев манипулятора, и рассматривать только 2 и 3 звенья, перенеся ось координат в точку стыковки 1 и 2 звеньев, получив в результате ранее рассмотренный случай задачи кинематики (Рис.4.5).
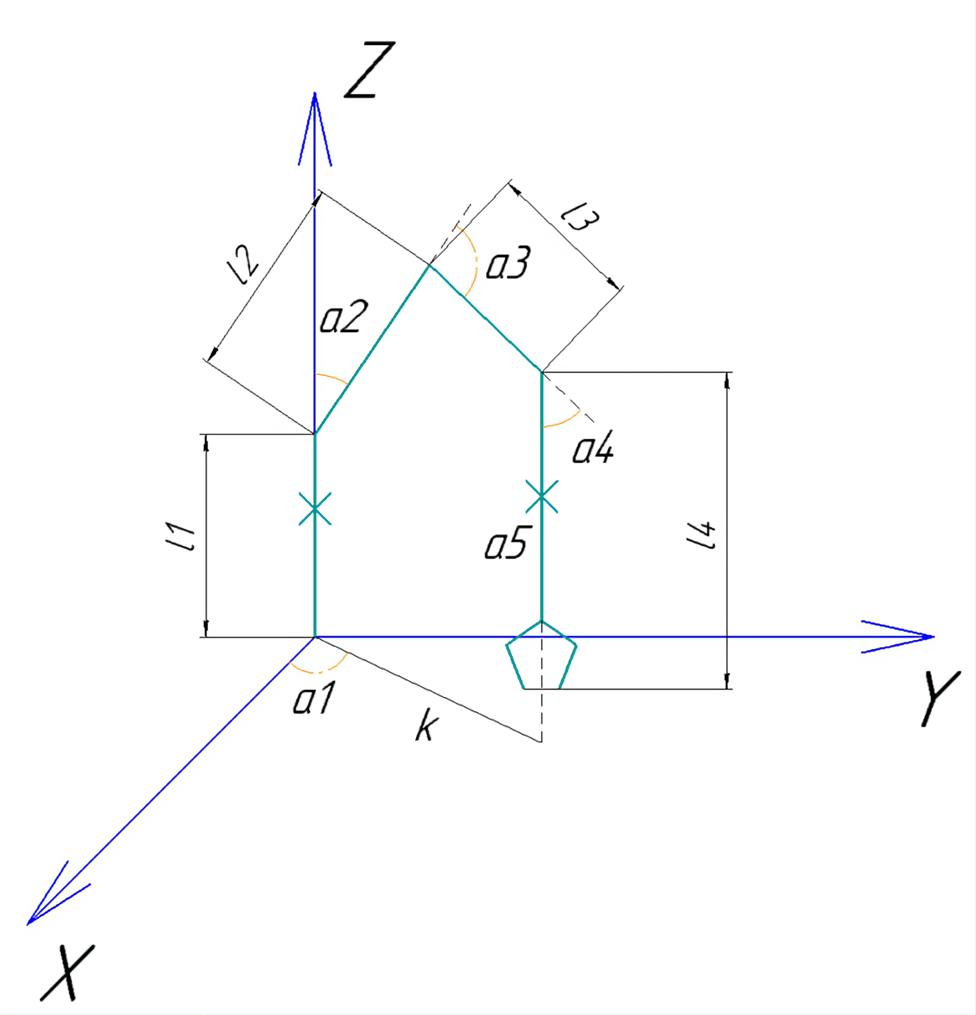
Рис. 4.3. Схема для решения обратной задачи кинематики
l1 = 102.50
l2 = 105
l3 = 80
l4 = 171.80
Рис. 4.4. Схема манипулятора
Обратная задача кинематики в данном случае будет решаться для точки А и относительно нововведенного начала координат, поэтому необходимо вычислить положение точки А относительно этого нового начала координат.
\(z_{реш}=z+l_4-l_1\)
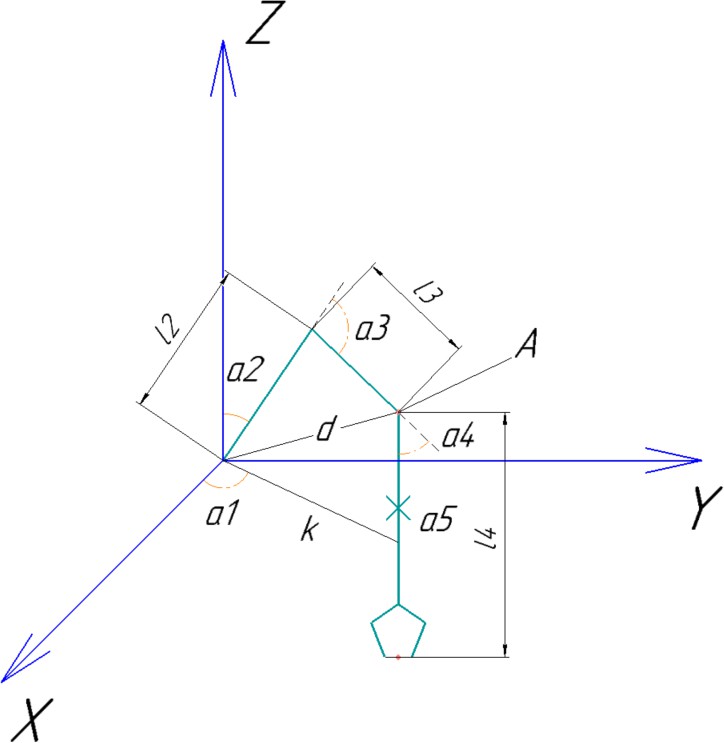
Рис. 4.5. Приведение кинематической схемы к известной
\(a_1=arctg(\frac{y}{x})\)
\(a_5=a_1\)
\(k=\sqrt {x^2+y^2}\)
\(d=\sqrt{k^2+z^2_p}\)
\(a_2=\frac {\pi}{2}-(arctg(\frac{z_p}{K})+arccos(\frac{d^2+l^2_2-l^2_3}{2*d*l_2}))\)
\(a_3=\pi-arccos(\frac{-d^2+l^2_2-l^2_3}{2*l_2*l_3})\)
\(a_4=\pi-(a_2+a_3)\)
Разработка управляющей программы
Для программирования манипулятора с угловой кинематикой используется то же самое программное обеспечение и такой же набор аппаратных средств, которые использовались для программирования манипулятора с плоско-параллельной кинематикой, рассматриваемого в учебном пособии «СТЕМ Мастерская. Часть 1»
Чтение позиций сервоприводов
Для чтения позиций всех сервоприводов манипулятора с угловой кинематикой можно использовать следующий пример:
#include <Dynamixel2Arduino.h>
#define DXL_SERIAL Serial3 //Последовательный порт DXL платы OpenCM9.04 EXP. (Чтобы использовать порт DXL на плате OpenCM 9.04, используйте Serial1 для Serial. И из-за кода драйвера OpenCM 9.04 используйте Serial1.setDxlMode(true); перед dxl.begin();.)
#define DEBUG_SERIAL Serial // Установка константы, отвечающей за последовательный порт, подключаемый к компьютеру
const uint8_t DXL_DIR_PIN = 22; // ПИН-код DIR платы STEM Board (Чтобы использовать порт DXL на плате OpenCM 9.04, используйте 28 для PIN-кода DIR.)
const float DXL_PROTOCOL_VERSION = 2.0; // инициализация переменной, отвечающей за протокол передачи данных от OpenCM9.04 к сервоприводам
Dynamixel2Arduino dxl(DXL_SERIAL, DXL_DIR_PIN); // инициализация указателя на команды из библиотеки Dynamixel
#define jointN 6 // задание количества ненулевых столбцов массива #define pages 3 // задание количества ненулевых строк массива
int i=0; // задание переменной-счетчика i
int j=1; // задание переменной-счетчика j
int buf[pages+1][jointN+1]={ // инициализация двумерного массива, его размер задается: 3+1=4 на 6+1=7, 4 на 7, так как в программировании нумерация
{0,0, 0, 0, 0, 0, 0}, // элементов начинается с 0, но нулевой элемент мы использовать не будем, в связи с чем начнем с первого
{0, 507, 492, 531, 498, 521, 626, },
{0, 506, 443, 403, 385, 607, 626, },
{0, 508, 532, 627, 613, 412, 626, },
};
void setup() {
// поместите код установки здесь, чтобы запустить:
DEBUG_SERIAL.begin(57600); // установка скорости обмена данными по последовательному порту компьютера
dxl.begin(1000000); // установка скорости обмена данными по последовательному порту манипулятора
dxl.setPortProtocolVersion(DXL_PROTOCOL_VERSION); // выбор протокола обмена данными
for (i=1; i<jointN+1; i++) // цикл с изменением i от 1 до 6 с шагом 1
{
dxl.setOperatingMode(i, OP_POSITION); // установка режима работы привода с номером i в качестве шарнира
}
}
void loop() {
// поместите свой основной код, чтобы запускать повторно:
for (j=1;j<=pages;j++) // цикл с изменением j от 1 до 6 с шагом 1
{
for(i=1;i<=jointN;i++) // цикл с изменением i от 1 до 6 с шагом 1
{
dxl.torqueOn(i); //подаем питание на i серву
dxl.setGoalVelocity(i, 50); // задание целевой скорости 50 сервоприводу с номером i
dxl.setGoalPosition(i, buf[j][i]); // задание целевого положения, получаемого из элемента ([j],[i]) сервоприводу с номером i
}
delay(5000);
}
}
Воспроизведение записанных позиций
Далее рассматривается программа, позволяющая воспроизводить позиции, которые ранее были считаны предыдущей программой. С помощью этой программы можно достичь цели – переноса небольшого предмета из одной точки стола в другую.
#include <Dynamixel2Arduino.h> // подключение библиотеки Dynamixel
#define DXL_SERIAL Serial3 // Последовательный порт DXL платы OpenCM9.04 EXP. (Чтобы использовать порт DXL на плате OpenCM 9.04, используйте Serial1 для Serial. И из-за кода драйвера OpenCM 9.04 используйте Serial1.setDxlMode(true); перед dxl.begin();.)
#define DEBUG_SERIAL Serial // Установка константы, отвечающей за последовательный порт, подключаемый к компьютеру
const uint8_t DXL_DIR_PIN = 22; // инициализация переменной, отвечающей за номер пина, подключенного к информационному пину сервоприводов манипулятора
const float DXL_PROTOCOL_VERSION = 2.0; // инициализация переменной, отвечающей за протокол передачи данных от OpenCM9.04 к сервоприводам
Dynamixel2Arduino dxl(DXL_SERIAL, DXL_DIR_PIN); // инициализация указателя на команды из библиотеки Dynamixel
#define jointN 6 // инициализация константы, обозначающей количество сервоприводов (и, соответственно, элементов массива)
int pos=0; // инициализация переменной
pos int i=0; // инициализация переменной i
int buf[jointN+1]; // инициализация одномерного массива, его размер задается 6+1=7, так как в программировании нумерация
// // элементов начинается с 0, но нулевой элемент мы использовать не будем, в связи с чем начнем с первого
//
void setup() {
//
/DEBUG_SERIAL.begin(57600); // установка скорости обмена данными по последовательному порту компьютера
dxl.begin(1000000); // установка скорости обмена данными по последовательному порту манипулятора
dxl.setPortProtocolVersion(DXL_PROTOCOL_VERSION); // выбор протокола обмена данными
for (i=1; i<jointN+1; i++) // цикл с изменением i от 1 до 6 с шагом 1
// {
dxl.setOperatingMode(i, OP_POSITION); // установка режима работы сервопривода с номером i в качестве шарнира
// }
//}
//
void loop() {
//
for (i=1; i<=jointN; i++) // цикл с изменением i от 1 до 6 с шагом 1
{
pos = dxl.getPresentPosition(i); // получение текущей позиции привода с номером i и запись в переменную pos
buf[i]=pos; // запись переменной значения pos в i-тый элемент массива buf
Serial.println(buf[i]);
}
Serial.print(«{0, «); //вывод в монитор порта текста «{0, «
for (i=1; i<=jointN; i++) // цикл с изменением i от 1 до 6 с шагом 1
{
Serial.print(buf[i]); // вывод в монитор порта значения ячейки массива с номером i
Serial.print(«, «); // вывод в монитор порта текста «, «
}
Serial.print(«}, «); // вывод в монитор порта текста «}, «
Serial.println(‘ ‘); // вывод в монитор порта текста « « и перенос курсора на следующую строку
//
delay(1000); // задержка, пауза в 1 секунду
}
Обратите внимание, в этой программе задается двумерный массив, в котором записаны положения сервоприводов. Построчно записаны различные положения манипулятора, а по столбцам – отдельные положения каждого из сервоприводов. Поэтому массив имеет 6 столбцов и переменное количество строк, которое зависит от количества воспроизводимых положений (на самом деле, число строк и столбцов на 1 больше, так как есть неиспользуемые нулевые строка и столбец; они задаются нулевыми).
В основной части программы при помощи двух циклов перебираются элементы массива. Соответствующие значения отправляются на сервоприводы для воспроизведения, в результате чего манипулятор будет отрабатывать положения, заданные в массиве. Положения в массив будут предварительно записаны самим пользователем с использованием предыдущей программы.
Таким образом, 2 программы, работающие в связке, позволят организовать копирующий режим работы манипулятора. Данный режим в рассматриваемом примере работает следующим образом:
Считывание и вывод на экран позиций (используется программа для чтения позиций).
Затем человек вручную задает некоторую позицию манипулятора (поворачивая манипулятор рукой и придерживая его при этом). В монитор порта через каждую секунду выводится текущая конфигурация манипулятора. Когда значения построчно начинают повторяться, то есть манипулятор вручную установлен в целевую позицию, в мониторе порта необходимо выключить автопрокрутку, а затем, выделив курсором одну из нужных строчек (обозначающих целевую позицию), скопировать эту строку (используя связку горячих клавиш Ctrl+C). Далее эту строку необходимо будет вставить в программу для воспроизведения позиций.
Эти действия нужно повторять до тех пор, пока все позиции для воспроизведения не будут записаны.
Воспроизведение позиций.
Когда все позиции считаны и записаны в массив, необходимо убедиться, что программа работает корректно. Это можно сделать, проведя компиляцию. Также необходимо следить за тем, чтобы переменная, отвечающая за количество строк в массиве, была задана верно – под именно текущее количество строк (а оно зависит от пользователя).
Таким образом, предварительно «научив» манипулятор переносить какой-либо предмет (последовательно задавая все положения манипулятора, необходимые для переноса предмета: начальное, наведение на предмет, подход к предмету, схват, перенос, опускание предмета, отпускание предмета), можно добиться того, что манипулятор будет воспроизводить позиции, которым он ранее научился.
SCARA-манипулятор DIY
SCARA-манипуляторы представляют собой механизмы с рычажной кинематикой, рабочий орган которых перемещается в одной плоскости за счет вращательного движения рычагов, на конце которых он расположен. Как правило, такие манипуляторы состоят из двух рычагов, соединенных в одной точке и двух независимых приводов, один из которых находится в точке соединения рычагов и вращает их друг относительно друга. Второй же привод находится в точке крепления рычага к основанию и вращает его относительно рабочей плоскости. Внешний вид такого манипулятора представлен на рисунке 4.6:
Рис. 4.6. Типичный промышленный SCARA-манипулятор
Обратная задача кинематики SCARA-манипулятора
Для запуска манипулятора необходимо научиться решать обратную (инверсную) кинематическую задачу. Исходя из известной позиции, в которую требуется переместить манипулятор робота (например, схватить объект, который находится на конвейере в точке с координатами x, y) требуется определить величины углов, на которые необходимо повернуть двигатели, связанные с рычагами робота, чтобы установить его в правильное положение для захвата. Примеры положений звеньев манипулятора при достижении рабочим органом требуемого положения представлены на рисунке 4.7
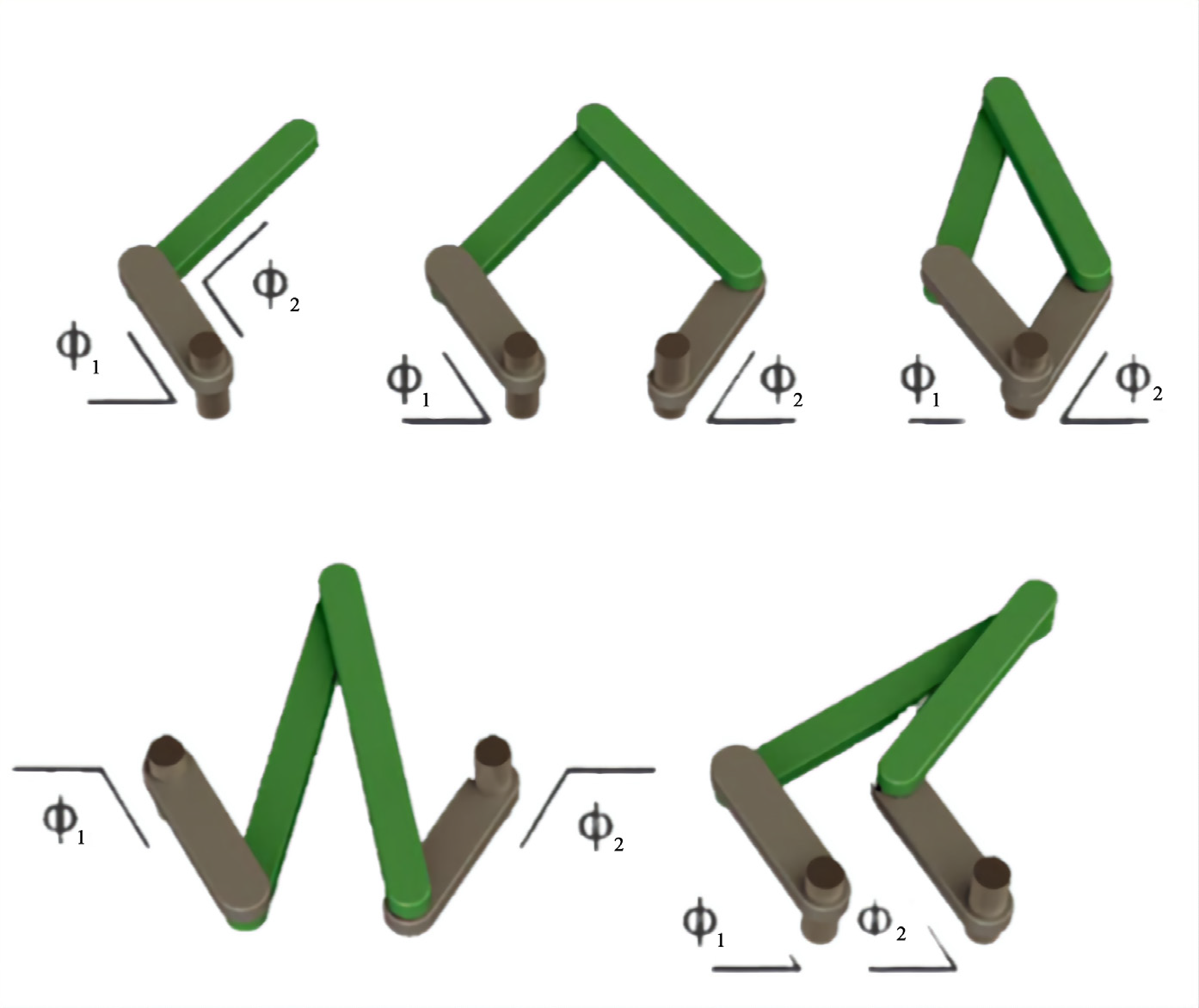
Рис. 4.7. Варианты положений рабочего органа манипулятора
Формализуем задачу: неподвижное основание и его движущиеся рычаги можно представить в виде отрезков, соединенных между собой шарнирами. Углы поворота рычагов робота обозначим как \(0_1\), \(0_2\),\(0_3\) а координаты точек конца каждого рычага \(Х_0,Х_1,Х_2 и Y_0, Y_1, Y_2,\) где в реальности будут закреплены сервопривода. Конечные координаты \(Х_3\) и \(Y_3\) нам известны. Это точка, в которую манипулятор должен прийти. Первый угол поворота рассматриваем от положительного направления оси Х до рычага. Последующие углы рассматриваются от предыдущего звена до рассматриваемого. Положительный угол поворота направлен против часовой стрелки.
Манипулятор SCARA имеет некоторую сложность с решением задачи. Это связано с тем, что для достижения конечной точки С могут способствовать различные положения манипулятора на плоскости.
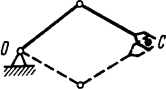
Рис. 4.8. Возможность положения звеньев манипулятора при достижения конечной точки
В данном случае, механизм обладает избыточными степенями подвижности – движение звеньев может осуществляться при неподвижном схвате, что позволяет преодолевать внешние препятствия или проводить работы в замкнутых объемах. Поэтому для неподвижности конечного звена со схватом необходимо ввести еще одну координату γ – это угол, под которым конечное звено должно подойти к предмету относительно положительного направления оси Х. Таким образом, неопределенность будет возникать только между первым и вторым звеном манипулятора. Эта проблема решается программным способом.
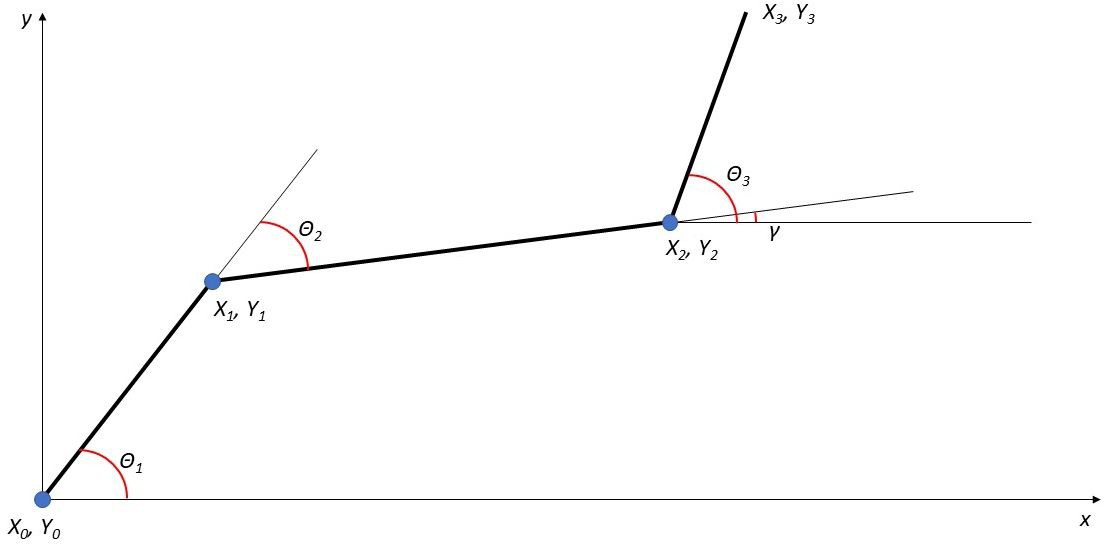
Рис. 4.9. Варианты положений рабочего органа манипулятора
Для решения задачи введем несколько ключевых параметров, которые определяются геометрическими размерами робота: длины звеньев \(l_1,l_2,l_3;\)угол подхода схвата к объекту относительно оси Х, γ. Решение задачи осуществляется в программе MathCad. Зададим раз-
меры звеньев:
\(l_1\) := 92
\(l_2\) := 66
\(l_3\) := 106
Укажем координаты, в которые должен прийти манипулятор, и угол, под которым он будет располагаться:
\(x_3\) := 264
\(y_3\) := 0
\(\varphi\) := 0 deg
После того, как необходимые данные введены, можем начать решение.
- Определим координаты конца второго звена:
\(x_2:=x_3-l_3*cos(\varphi)\)
\(y_2:=y_3-l_3*sin(\varphi)\)
- Найдем координаты конца первого звена. Для этого составим систему уравнений двух окружностей. Центр координат первой окружности находится в начале системы координат (0,0), а её радиус равен длине первого звена l1. Центр второй окружности находится в координатах конца второго звена (Х2, Y2), а её радиус равен l2. Найдем координаты пересечения этих двух окружностей. В результате получим квадратное уравнение и два корня. Приведем решение в программе MathCad:
\(a:=x^2_2+l^2_1+y^2_2-l^2_2\)
\(D:=(4*x_2*a)^2-4*(-4*y^2_2-4*x^2_2)*(-a^2+4*l^2_1*y^2_2)=0\)
\(x_{11}:=\frac{(-4*x_2*a-\sqrt D)}{[2*(-4*y^2_2-4*x^2_2)]}=92\)
\(x_{12}:=\frac{(-4*x_2*a-\sqrt D)}{[2*(-4*y^2_2-4*x^2_2)]}=92\)
В данном случае решение одинаковое, так как D = 0, а пересечение окружностей осуществляется лишь в одной точке.
- Теперь можно найти угол поворота первого звена для двух вариантов:
\(fi_{11}:=a cos(\frac{x_11}{l_1}=0*deg)\)
\(fi_{12}:=a cos(\frac{x_12}{l_1}=0*deg)\)
- Найдем координаты \(Y\) конца первого звена двух вариантов:
\(y_{11}:=\sqrt {l^2_1-x^2_{11}}=0\)
\(y_{12}:=\sqrt {l^2_1-x^2_{12}}=0\)
- Далее рассчитаем длину проекции второго звена на оси:
\(x_{21}:=x_2-x_{11}=66\) \(x_{22}:=x_2-x_{12}=66\) \(y_{21}:=y_2-y_{11}=66\) \(y_{22}:=y_2-y_{12}=66\)
- Следующим шагом вычислим углы наклона проекции второго звена к оси Х:
\(t_{21}:=a tan2(x_{21},y_{21})=0*deg\)
\(t_{22}:=a tan2(x_{22},y_{22})=0*deg\)
Напомним, что данная функция определяется следующим образом:
\(\(-\pi\leq a tan2(a,b)\leq\pi\)\) Т.е. она учитывает принадлежность аргументов к одному из четырех квадрантов.
- Определив разницу между углом наклона первого звена и второго, можно вычислить угол поворота второго звена относительно первого:
\(fi_{21}:=t_{21}-fi_{11}=0*deg\) \(fi_{22}:=t_{22}-fi_{12}=0*deg\) 8. Произведем рассчет для нахождения третьего угла поворота:
\(fi_{31}:=\varphi-fi_{11}-fi_{21}\) \(fi_{32}:=\varphi-fi_{12}-fi_{22}\)
- Необходимо сделать преобразование координат, поскольку наша декартовая система отличается от системы координат робота. Это связано с тем, что 0° для сервоприводов находится в другом положении от нашего представления. Координатная плоскость робота представлена на рис. 4.10.
Таким образом, обратная задача кинематики была решена. Теперь необходимо разработать систему управления манипулятором с использованием управляющего микроконтроллера.
Рис. 4.10. Координатная плоскость робота
Устройство SCARA-манипулятора
Инструкция по сборке робота, а также исходные файлы конструктивных элементов под лазерную резку находятся в свободном доступе и доступны для скачивания с официального сайта appliedrobotics.ru из раздела «Учебные материалы». Между каждым звеном установим три сервопривода. В качестве управляющего контроллера используется Arduino-подобная аппаратная платформа OpenCM, установленная на периферийной плате расширения STEM Board. Питание обеспечивается с помощью либо стандартного LiPo аккумулятора, выдающего номинальное напряжение в 11,1 В, либо через сетевой адаптер питания. Соединение сервоприводов рекомендуется выполнить последовательно и подключить получившуюся цепь к плате расширения, как на рисунке 4.11.
Также работ имеет подвижное конечно звено, которое перемещается в плоскости, перпендикулярной к основным звеньям. Оно будет управляться отдельно.
Перед тем, как приступить к разработке управляющей программы, необходимо уточнить ID сервоприводов, установленных на манипуляторе. ID сервоприводов указаны на рисунке 4.11.
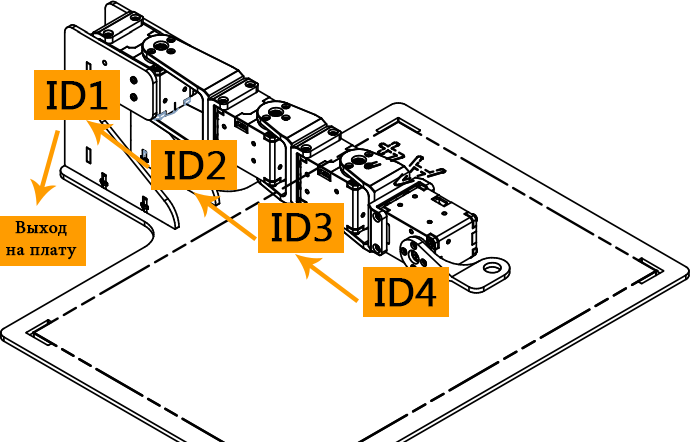
Рис. 4.11. Схема подключения сервоприводов и их ID
Для уточнения и установки ID сервоприводов можно использовать стандартные примеры из Arduino IDE с установленной поддержкой платы OpenCM9.04. Для этого необходимо открыть два примера под названием: “o_Find_Dynamixel” и “c_ID_Change”. (“Файл“ => “Примеры“ => OpenCM9.04 => DynamixelWorkbench).
С помощью примера “o_Find_Dynamixel” можно узнать текущее ID сервопривода следующим образом: сервопривод подключается к плате, подключается питание и загружается пример на плату. После чего в Мониторе порта можно увидеть информацию о текущем значении ID, которое необходимо запомнить.
После этого нужно открыть второй пример - “c_ID_Change”. В оглавлении, при необходимости, нужно изменить эти строки:
#define DXL_ID 1 // 1 – это текущее значение ID сервопривода
#define NEW_DXL_ID 2 // 2 – это значение, на которое требуется поменять ID
Помимо этого, в обоих случаях необходимо поменять скорость “общения” платы со входами Dynamixel
#define BAUDRATE 57600 // изменяем значение на 1 000 000
Таким образом, устанавливаются необходимые ID для сервоприводов.
Для обеспечения безопасной работы рекомендуется перед запуском определить, в каком положении находится вал сервопривода при 0°.
Рис. 4.12. SCARA-манипулятор
Разработка управляющей программы
В модели данного робота в качестве управляющего контроллера используется Arduino-подобный контроллер OpenCM. Для работы с ним используется среда разработки Arduino IDE.
Для работы с Dynamixel подключаем библиотеку и инициализируем переменные:
#include <DynamixelWorkbench.h>
Для обмена данных по протоколу Dynamixel в коде программы необходимо указать номер аппаратной шины – другими словами порты, на плате, к которым будет выполнено подключение сервоприводов.
#if defined( OPENCM904 )
#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-OpenCM 485EXP
#elif defined( OPENCR )
#define DEVICE_NAME «»
#endif
В рассматриваемом примере требуется выбрать 3 вариант Указываем скорость обмена данными через порт подключения
#define BAUDRATE 1000000 // Скорость передачи данных
Далее необходимо указать ID сервоприводов, которыми необходимо управлять. Все это делается в коде программы до функции setup() при помощи следующих команд:
#define DXL_ID1 1 // адрес сервопривода DYNAMIXEL
#define DXL_ID2 2
#define DXL_ID3 3
#define DXL_ID4 4
Инициализируем геометрические данные робота в качестве глобальных переменных. Они нам необходимы для расчетов. В рассматриваемой модели робота нужно проинициализировать следующие переменные:
DynamixelWorkbench dxl_wb;
float theta1, theta2, theta3;
float m = 0;
float n = 0;
float k= 0;
float t = 0;
float l1 = 92;
float l2 = 66;
float l3 = 106;
float x11;
bool flag = false;
Функция setup()
Зададим переменные model_number и присвоим им ID сервоприводов. После этого производим подключение всех сервоприводов манипулятора.
void setup() {
const char *log ;
Serial.begin(57600);
uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;
dxl_wb.init(DEVICE_NAME, BAUDRATE, &log);
dxl_wb.ping(DXL_ID1, &model_number1, &log);
dxl_wb.ping(DXL_ID2, &model_number2, &log);
dxl_wb.ping(DXL_ID3, &model_number3, &log);
dxl_wb.ping(DXL_ID4, &model_number4, &log);
dxl_wb.jointMode(DXL_ID1, 1, 1, &log);
dxl_wb.jointMode(DXL_ID2, 1, 1, &log);
dxl_wb.jointMode(DXL_ID3, 1, 1, &log);
dxl_wb.jointMode(DXL_ID4, 1, 1, &log);
}
Функция find_angle(float x, float y, float a)
В данной функции происходит решение обратной задачи. Входные данные:
x – координата схвата по оси Х y - координата схвата по оси Y
a – угол относительно оси Х, под которым необходимо, чтобы схват подошел к объекту
void find_angle(float x, float y, float a)
{
float x2 = x - l3*cos(a); // Нахождение координат конца второго звена
float y2 = y - l3*sin(a);
float d = sqrt(x2*x2 + y2*y2); // Введем параметр
if (d > (l1+l2)) // Проверка дискриминанта
{
Serial.println(«Out of zone»); // Если значение дискриминанта меньше нуля, манипулятор занимает базовое положение
theta1 = 0;
theta2 = 0;
theta3 = 0;
}
else
{
if (y < 0 && a <= 0 )
{
y = -y;
a = -a;
flag = true;
}
float A = ((l1*l1)-(l2*l2)+(d*d))/(d*2);
float alfa = acos(x2/d);
float delta = acos(A/l1);
float q1 = alfa - delta;
float x1 = l1*cos(q1);
float y1 = l1*sin(q1);
float q2 = acos((x2-x1)/l2);
theta1 = q1;
theta2 = q2-q1;
theta3 = a-q1-theta2;
if(flag)
{
Serial.println(«FLAG»);
theta1 = -theta1;
theta2 = -theta2;
theta3 = -theta3;
flag = false;
}
}
}
Функция set_pos()
В данной функции осуществляется задание угла поворота вала двигателя на манипуляторе
void set_pos( float p1 , float p2, float p3, float p4, int del)
// Функция для задания угла поворота вала двигателя на манипулятора в радианах
{
dxl_wb.goalPosition(DXL_ID1,p1);
dxl_wb.goalPosition(DXL_ID2,p2);
dxl_wb.goalPosition(DXL_ID3,p3);
dxl_wb.goalPosition(DXL_ID4,p4);
delay(del);
}
Функция loop()
Рассмотрим функцию loop(), которая представляет собой бесконечный цикл.
void loop() {
if (Serial.available() > 0 ) {
m = Serial.parseInt();
n = Serial.parseInt();
k = Serial.parseInt();
find_angle(m, n, k );
Serial.print(«Angle #1: « );
Serial.println(theta1*180/3.14);
Serial.print(«Angle #2: « );
Serial.println(theta2*180/3.14);
Serial.print(«Angle #3: « );
Serial.println(theta3*180/3.14);
}
set_pos(theta1, theta2, theta3, 0, 700); // Поворот валов приводов на вычисленный угол – достижение заданных координат
}
Также можно корректировать положения робота в реальном времени. С помощью консоли пользователь вручную может вводить координаты, которые будет занимать робот.
Координаты вводятся в миллиметрах. Значения можно вводить через любые знаки препинания, главное вводить их в правильном порядке и разделять пробелом.
В результате, код управляющей программы будет выглядеть следующим образом:
#include <DynamixelWorkbench.h>
#if defined( OPENCM904 )
#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-STEM Board
#elif defined( OPENCR )
#define DEVICE_NAME «»
#endif
#define BAUDRATE 1000000 // Скорость передачи данных
#define DXL_ID1 1 // адрес сервопривода DYNAMIXEL
#define DXL_ID2 2
#define DXL_ID3 3
#define DXL_ID4 4
DynamixelWorkbench dxl_wb;
float theta1, theta2, theta3;
float m = 0;
float n = 0;
float k= 0;
float t = 0;
float l1 = 92;
float l2 = 66;
float l3 = 106;
float x11;
bool flag = false;
void set_pos( float p1 , float p2, float p3, float p4, int del)
// Функция для задания угла поворота вала двигателя на манипулятора в радианах
{
dxl_wb.goalPosition(DXL_ID1,p1);
dxl_wb.goalPosition(DXL_ID2,p2);
dxl_wb.goalPosition(DXL_ID3,p3);
dxl_wb.goalPosition(DXL_ID4,p4);
delay(del);
}
void find_angle(float x, float y, float a)
{
float x2 = x - l3*cos(a);
float y2 = y - l3*sin(a);
float d = sqrt(x2*x2 + y2*y2);
if (d > (l1+l2))
{
Serial.println(«Out of zone»);
theta1 = 0;
theta2 = 0;
theta3 = 0;
}
else
{
if (y < 0 && a <= 0 )
{
y = -y;
a = -a;
flag = true;
}
float A = ((l1*l1)-(l2*l2)+(d*d))/(d*2);
float alfa = acos(x2/d);
float delta = acos(A/l1);
float q1 = alfa - delta;
float x1 = l1*cos(q1);
float y1 = l1*sin(q1);
float q2 = acos((x2-x1)/l2);
theta1 = q1;
theta2 = q2-q1;
theta3 = a-q1-theta2;
if(flag)
{
Serial.println(«FLAG»);
theta1 = -theta1;
theta2 = -theta2;
theta3 = -theta3;
flag = false;
}
}
}
void setup() {
const char *log ;
Serial.begin(57600);
uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;
dxl_wb.init(DEVICE_NAME, BAUDRATE, &log);
dxl_wb.ping(DXL_ID1, &model_number1, &log);
dxl_wb.ping(DXL_ID2, &model_number2, &log);
dxl_wb.ping(DXL_ID3, &model_number3, &log);
dxl_wb.ping(DXL_ID4, &model_number4, &log);
dxl_wb.jointMode(DXL_ID1, 1, 1, &log);
dxl_wb.jointMode(DXL_ID2, 1, 1, &log);
dxl_wb.jointMode(DXL_ID3, 1, 1, &log);
dxl_wb.jointMode(DXL_ID4, 1, 1, &log);
}
void loop() {
if (Serial.available() > 0 ) {
m = Serial.parseInt();
n = Serial.parseInt();
k = Serial.parseInt();
k = (k*3.14)/180;
find_angle(m, n, k );
Serial.print(«Angle #1: « );
Serial.println(theta1*180/3.14);
Serial.print(«Angle #2: « );
Serial.println(theta2*180/3.14);
Serial.print(«Angle #3: « );
Serial.println(theta3*180/3.14);
}
set_pos(theta1, theta2, theta3, 0, 700);
}
STEWART-платформа DIY
STEWART - платформа (платформа Стюарта) представляет собой один из видов параллельного манипулятора, имеющего 6 степеней свободы. Отличительной особенностью данного вида манипуляторов является компоновка его сервоприводов – все сервопривода располагаются в одной плоскости тремя парами, что приводит к созданию шести тяг на шарнирных соединителях (Рис. 4.13).
Рабочий орган такого манипулятора чаще всего представляется в виде горизонтальной платформы, на котором размещается объект. За счет большого количества тяг становится возможно точное и быстрое изменение положения находящегося на платформе объекта в пространстве. Вследствие чего, платформы Стюарта используются в задачах, где необходимо точное позиционирование объекта в пространстве.
Рис. 4.13. Типовая модель платформы Стюарта
Обратная задача кинематики
Для запуска платформы необходимо научиться решать обратную (инверсную) кинематическую задачу. Исходя из требуемой позиции, в которую необходимо переместить платформу (например, для удержания в равновесии объекта, находящегося на платформе) требуется определить величины углов, на которые необходимо повернуть фланцы сервоприводов, связанные с тягами манипулятора, чтобы установить его платформу в правильное положение. Платформа является одним из видов параллельного манипулятора, имеющим шесть степеней свободы и координаты, по которым она может передвигаться линейное перемещение по осям \(X,Y,Z,\) а также углы поворота: крен (Θ), тангаж (φ) и рысканье (ψ).
Манипулятор состоит из двух основных частей: неподвижной плоскости – базы, и подвижной плоскости – платформы. На базе находятся шесть сервоприводов, к фланцам которых прикреплены рычаги. В свою очередь, усилие от рычагов передается на тяги через шарнирные соединители, которые так же имеют шарнирное соединение с подвижной частью манипулятора.
Решение обратной задачи необходимо начать с размещения в центре основания точки отсчета системы координат с осями \(х, у, z\). В таком случае, платформа будет иметь свою подвижную систему координат \(х’,у’,z’\). Платформа определяется с помощью трех поступательных перемещений вдоль осей \(х, у, z\) относительно основания. Три угла поворота вокруг осей определяют ориентацию платформы по отношению к основанию: поворот на угол \(ψ\) вокруг оси \(z\), поворот на угол \(Θ\) вокруг оси \(у\), поворот на угол \(φ\) вокруг оси \(х\).
Рассмотрим поворот относительно оси \(z\) на угол \(ψ\). Тогда матрица вращения \(Rz(y)\) имеет вид:
Аналогично, имеем матрицу вращения для поворота вокруг оси у на угол \(Θ\):
Для третьего поворота на угол \(φ\) вокруг оси \(х\) имеем:
Полная матрица вращения платформы по отношению к основанию определяется по следующей формуле:
Теперь рассмотрим i-тую тягу платформы Стюарта (Рис.4.14).
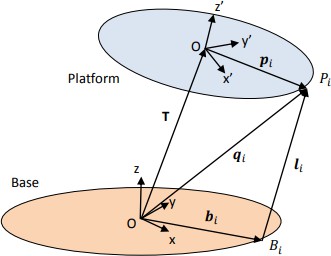
Рис. 4.14. Рассмотрение i-той тяги платоформы Стюарта
Координаты qi точки соединения верхней точки Pi относительно системы координат основания задаются уравнением:
\(q_1=T+{}^pR_b*p_i\)
Здесь вектор T описывает линейное перемещение начала координат платформы по отношению к системе координат основания, pi – является вектором, определяющим координаты точки соединения Pi относительно системы координат платформы.
Аналогичным образом задается длина i-ой тяги в следующем виде:
\(l_i=T+{}^pR_b*p_i-b_i\)
где bi – вектор, определяющий координаты нижней точки Bi соединения тяги. С помощью 6 уравнений определяют длины 6 тяг, таким образом, определяется положение и ориентация платформы.
Далее необходимо определить угол поворота вала сервопривода. При нахождении формулы использовались следующие обозначения (Рис. 4.15):
а – длина рычага сервопривода,
Аi – точки соединения рычага с нижней точкой стержня i-го сервопривода с координатами а = [xa, ya, za] в системе координат основания,
Вi – точки вращения центра рычага сервопривода с координатами b = [xb, yb, zb] в системе основания,
Pi – точки соединения верхнего шарнира стержня с платформой, с координатами р = [xр, yр, zр] в системе координат платформы,
S – длина стержня,
li = длина i-ого стержня,
α – угол между рычагом сервопривода и горизонталью,
β – угол между рычагом сервопривода и осью х После некоторых преобразований имеем:
\(a=sin^-1\frac{L}{\sqrt M^2+N^2}-tan^-1\frac{N}{M}\)
где
$$ L=l^2-(s^2-a^2) $$ $$ M=2a(z_p-z_b) $$ $$ N=2a[cos\beta(x_p-x_b)+sin\beta(y_p-_b)] $$ При расчете объявим все константы и приведем платформу в базовое положение, при котором все рычаги будут стоять параллельно базе.
\(s := 211\) \(\psi := 0 deg\) \(x := 0\)
\(p := 110\) \(е := 0 deg\) \(y := 0\)
\(a := 35\) \(\varphi := 0 deg\) \(z := 200\)
\(b := 100\)
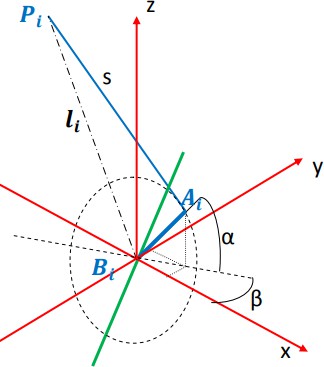Рис. 4.15. Схема расчета угла поворота вала сервопривода
Найдем проекции точек b и p на оси X и Y:
\(b_{1x} := b*cos(0.61) = 81.965\) \(p_{1x} := p*cos(0.13) = 109.072\)
\(b_{1y} := b*sin(0.61) = 57.287\) \(p_{1y} := p*sin(0.13) = 14.26\)
\(b_{2 x} := b*cos(1.48) = 9.067\) \(p_{2 x} := p*cos(1.95) = -40.72\)
\(b_{2 y} := b*sin(1.48) = 99.588\) \(p_{2 y} := p*sin(1.95) = 102.186\)
\(b_{3x} := b*cos(2.7) = -90.407\) \(p_{3x} := p*cos(2.22) = -66.501\)
\(b_{3 y} := b*sin(2.7) = 42.738\) \(p_{3 y} := p*sin(2.22) = 87.622\)
\(b_{4 x} := b*cos(3.58) = -90.543\) \(p_{4 x} := p*cos(4.04) = -68.514\)
\(b_{4 y} := b*sin(3.58) = -42.45\) \(p_{4 y} := p*sin(4.04) = -86.057\)
\(b_{5x} := b*cos(4.8) = 8.75\) \(p_{5x} := p*cos(4.31) = -43.078\)
\(b_{5 y} := b*sin(4.8) = -99.616\) \(p_{5 y} := p*sin(4.31) = -101.214\)
\(b_{6 x} := b*cos(5.6) = 77.557\) \(p_{6 x} := p*cos(6.13) = 108.712\)
\(b_{6 y} := b*cos(5.6) = -63.127\) \(p_{6 y} := p*cos(6.13) = -16.785\)
Найдем матрицу поворота:
Найдем вектор l1:
Найдем длину вектора l1:
Рассчитаем оставшиеся компоненты для конечной формулы:
Небольшая ошибка присутствует из-за округлений и неточности измерения базовой высоты в 200 мм. Из-за конструкции в дальнейшем перед нечетными углами поворота необходимо ставить знак “ - ” для вращения в противоположную сторону.
Расчет для оставшихся пяти сервоприводов аналогичен.
Устройство платформы STEWART
Инструкция по сборке робота, а также исходные файлы конструктивных элементов под лазерную резку находятся в свободном доступе и доступны для скачивания с официального сайта appliedrobotics.ru из раздела «Учебные материалы». Сборка платформы Стюарта представляет собой размещение 6 сервоприводов на базе, установке на их фланцы рычагов и соединение подвижной платформы с рычагами через тяги с использованием шарнирного соединения. Перед установкой рычага необходимо перевести сервопривода в нулевое положение и присоединить рычаг параллельно базе. Также необходимо обратить внимание, что соседние рычаги располагаются навстречу друг другу в базовом положении. Тяги должны располагаться, как показано на рисунке 4.15.
В качестве управляющего контроллера используется Arduino-подобная аппаратная платформа OpenCM, установленная совместно со встраиваемой платой NanoPi-AR на плате расширения STEM Board. Питание обеспечивается либо при помощи стандартного LiPo аккумулятора, выдающего номинальное напряжение в 11,1 В, либо через сетевой адаптер питания. Соединение сервоприводов рекомендуется выполнить последовательно и подключить получившуюся цепь к плате расширения STEM Board как показано на Рис. 4.16.
Перед тем как приступить к разработке управляющей программы, необходимо уточнить ID сервоприводов, установленных на манипуляторе. ID сервоприводов указаны на следующей схеме, приведенной на рисунке 4.16.
Для уточнения и установки ID сервоприводов можно использовать стандартные примеры из Arduino IDE с установленной поддержкой платы OpenCM9.04. Для этого необходимо открыть два примера под названием: “o_Find_Dynamixel” и “c_ID_Change”. (“Файл“ => “Примеры“ => OpenCM9.04 => DynamixelWorkbench). С помощью примера “o_Find_ Dynamixel” можно узнать текущее ID сервопривода следующим образом: сервопривод подключается к плате, к нему подключается питание, после чего на контроллер загружается пример. После чего в Мониторе порта сможем увидеть информацию о текущем значении ID, которое необходимо запомнить.
Теперь необходимо открыть второй пример “c_ID_Change”. В оглавлении, при необходимости, нужно изменить эти строки:
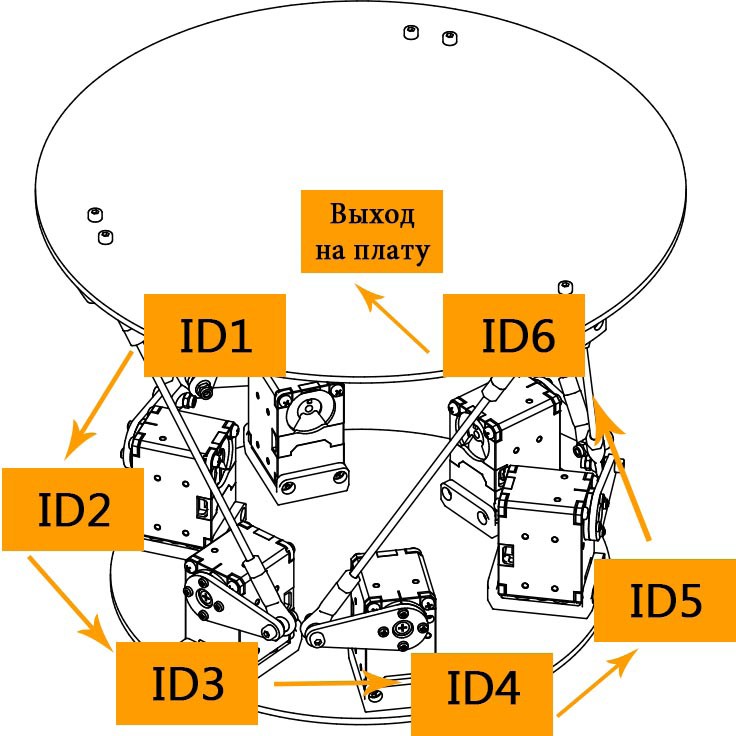
Рис. 4.16. Схема подключения сервоприводов и их ID
#define DXL_ID 1 // 1 – это текущее значение ID сервопривода #define NEW_DXL_ID 2 // 2 – это значение, на которое требуется поменять ID
#define BAUDRATE 57600 // изменяем значение на 1 000 000 Таким образом, устанавливаются необходимые ID для сервоприводов.
Для обеспечения безопасной работы, рекомендуется перед запуском определить, в каком положении находится вал сервопривода в положении 0°.
Разработка управляющей программы
В модели данного робота в качестве управляющего контроллера используется контроллер OpenCM. Для работы с ним используется среда разработки Arduino IDE.
Для работы с Dynamixel подключаем библиотеку и инициализируем переменные:
#include <DynamixelWorkbench.h>
После чего подключаем библиотеку для работы с математическими выражениями
#include <math.h>
Для обмена данных по протоколу Dynamixel в коде программы необходимо указать аппаратную шину. Другими словами, порты на плате, к которым будет выполнено подключение сервоприводов.
#if defined( OPENCM904 )
#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-OpenCM 485EXP
#elif defined( OPENCR )
#define DEVICE_NAME «»
#endif
Указываем скорость обмена данными через порт подключения:
#define BAUDRATE 1000000
Далее необходимо указать ID сервоприводов, которыми необходимо управлять. Все это делается в коде программы до функции setup() при помощи следующих команд:
#define DXL_ID1 1
#define DXL_ID2 2
#define DXL_ID3 3
#define DXL_ID4 4
#define DXL_ID5 5
#define DXL_ID6 6
DynamixelWorkbench dxl_wb;
Инициализируем геометрические данные робота в качестве глобальных переменных. Они нам необходимы для расчетов. В рассматриваемой модели робота инициализируем следующие переменные:
float s = 211;
float a = 35;
float b = 100;
float p = 110;
float fi_b = 0.61;
float fi_p = 0.13;
float bx, by, px, py;
float R[3][3];
float alfa1 = 0;
float beta1 = 0;
float gama1 = 0;
float x1;
float y_1;
float z1;
float angle0, angle1, angle2, angle3,angle4, angle5, angle6;
Функция setup()
Создаем переменные model_number и присваиваем им номер сервопривода. После производим подключение всех сервоприводов манипулятора.
void setup()
{
const char *log ;
Serial.begin(1000000);
uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;
uint16_t model_number5 = 5;
uint16_t model_number6 = 6;
dxl_wb.init(DEVICE_NAME, BAUDRATE, &log); dxl_wb.ping(DXL_ID1, &model_number1, &log); dxl_wb.ping(DXL_ID2, &model_number2, &log); dxl_wb.ping(DXL_ID3, &model_number3, &log); dxl_wb.ping(DXL_ID4, &model_number4, &log); dxl_wb.ping(DXL_ID5, &model_number5, &log); dxl_wb.ping(DXL_ID6, &model_number6, &log);
dxl_wb.jointMode(DXL_ID1, 20, 20, &log);
dxl_wb.jointMode(DXL_ID2, 20, 20, &log);
dxl_wb.jointMode(DXL_ID3, 20, 20, &log);
dxl_wb.jointMode(DXL_ID4, 20, 20, &log);
dxl_wb.jointMode(DXL_ID5, 20, 20, &log);
dxl_wb.jointMode(DXL_ID6, 20, 20, &log);
}
Теперь рассмотрим действие каждой функции отдельно.
Функция matrix(float alfa, float beta, float gama)
В данной функции находится матрица поворота, которая соответствует уравнению:
void matrix(float alfa, float beta, float gama)
{
R[0][0] = cos(alfa)*cos(beta);
R[1][0] = -sin(alfa)*cos(gama) + cos(alfa)*sin(beta)*sin(gama); R[2][0] = sin(alfa)*sin(gama) + cos(alfa)*sin(beta)*cos(gama); R[0][1] = sin(alfa)*cos(beta);
R[1][1] = cos(alfa)*cos(gama) + sin(alfa)*sin(beta)*sin(gama); R[2][1] = -cos(alfa)*sin(gama) + sin(alfa)*sin(beta)*cos(gama); R[0][2] = -sin(beta);
R[1][2] = cos(beta)*sin(gama);
R[2][2] = cos(beta)*cos(gama);
}
Функция angle(float fi_b, float fi_p, float x, float y, float z)
При помощи данной функции можно определить угол поворота для i-го рычага
void angle(float fi_b, float fi_p, float x, float y, float z)
{
bx = b*cos(fi_b);
by = b*sin(fi_b);
px = p*cos(fi_p);
py = p*sin(fi_p);
float A = R[0][0]*px + R[1][0]*py;
float B = R[0][1]*px + R[1][1]*py;
float C = R[0][2]*px + R[1][2]*py ;
A = A - bx + x;
B = B - by + y;
C = C + z;
float l = sqrt(A*A + B*B + C*C);
float L = l*l - s*s + a*a;
float M = 2*a*l;
float N = 2*a*(cos(fi_b)*(px - bx) + sin(fi_b)*(py - by));
angle0 = -(asin(L/(sqrt(M*M + N*N))) - atan(N/M));
}
Функция set_pos(float p1 , float p2, float p3, float p4, float p5, float p6,int del)
В данной функции осуществляется задание угла поворота вала двигателя на манипуляторе
void set_pos( float p1 , float p2, float p3, float p4, float p5, float p6, int del)
{
dxl_wb.goalPosition(DXL_ID1,p1); dxl_wb.goalPosition(DXL_ID2,p2); dxl_wb.goalPosition(DXL_ID3,p3); dxl_wb.goalPosition(DXL_ID4,p4); dxl_wb.goalPosition(DXL_ID5,p5); dxl_wb.goalPosition(DXL_ID6,p6);
delay(del);
}
Функция loop()
Теперь рассмотрим функцию loop(), которая представляет собой бесконечный цикл. Через нее можно корректировать положения робота в реальном времени. С помощью консоли пользователь может вручную вводить координаты, которые будет занимать робот.
void loop()
{
if (Serial.available() > 0 ) {
x1 = Serial.parseInt();
y_1 = Serial.parseInt();
z1 = Serial.parseInt();
alfa1 = Serial.parseInt();
beta1 = Serial.parseInt();
gama1 = Serial.parseInt();
Serial.print(«X = « );
Serial.println(x1);
Serial.print(«Y = « );
Serial.println(y_1);
Serial.print(«Z = « );
Serial.println(z1);
Serial.print(«Alfa = « ); Serial.println(alfa1);
Serial.print(«Beta = « ); Serial.println(beta1);
Serial.print(«Gamma = « ); Serial.println(gama1);
alfa1 = alfa1*3.14/180;
beta1 = beta1*3.14/180;
gama1 = gama1*3.14/180;
matrix(alfa1, beta1, gama1);
angle(0.61, 0.13, x1, y_1, z1);
angle1 = angle0;
angle(1.48, 1.95, x1, y_1, z1);
angle2 = -angle0;
angle(2.7, 2.22, x1, y_1, z1);
angle3 = angle0;
angle(3.58, 4.04, x1, y_1, z1);
angle4 = -angle0;
angle(4.8, 4.31, x1, y_1, z1);
angle5 = angle0;
angle(5.6, 6.13, x1, y_1, z1);
angle6 = -angle0;
Serial.print(«Angle #1: « ); Serial.println(angle1);
Serial.print(«Angle #2: « ); Serial.println(angle2);
Serial.print(«Angle #3: « ); Serial.println(angle3);
Serial.print(«Angle #4: « ); Serial.println(angle4);
Serial.print(«Angle #5: « ); Serial.println(angle5);
Serial.print(«Angle #6: « ); Serial.println(angle6);
set_pos(angle1, angle2, angle3, angle4, angle5, angle6, 50);
}
}
Координаты вводятся в миллиметрах. Значения можно вводить через любые знаки препинания, но в правильном порядке, и разделяя их пробелом.
В результате, код управляющей программы будет выглядеть следующим образом:
#include <DynamixelWorkbench.h>
#include <math.h>
#if defined( OPENCM904 )
#define DEVICE_NAME «3» //Dynamixel on Serial3(USART3) <-OpenCM 485EXP
#elif defined( OPENCR )
#define DEVICE_NAME «» #endif
#define BAUDRATE 1000000
#define DXL_ID1 1
#define DXL_ID2 2
#define DXL_ID3 3
#define DXL_ID4 4
#define DXL_ID5 5
#define DXL_ID6 6
DynamixelWorkbench dxl_wb;
float s = 211;
float a = 35;
float b = 100;
float p = 110;
float fi_b = 0.61;
float fi_p = 0.13;
float bx, by, px, py;
float R[3][3];
float alfa1 = 0;
float beta1 = 0;
float gama1 = 0;
float x1;
float y_1;
float z1;
float angle0, angle1, angle2, angle3, angle4, angle5, angle6;
void set_pos( float p1 , float p2, float p3, float p4, float p5, float p6, int del)
{
dxl_wb.goalPosition(DXL_ID1,p1);
dxl_wb.goalPosition(DXL_ID2,p2);
dxl_wb.goalPosition(DXL_ID3,p3);
dxl_wb.goalPosition(DXL_ID4,p4);
dxl_wb.goalPosition(DXL_ID5,p5);
dxl_wb.goalPosition(DXL_ID6,p6);
delay(del);
}
void matrix(float alfa, float beta, float gama)
{
R[0][0] = cos(alfa)*cos(beta);
R[1][0] = -sin(alfa)*cos(gama) + cos(alfa)*sin(beta)*sin(gama);
R[2][0] = sin(alfa)*sin(gama) + cos(alfa)*sin(beta)*cos(gama);
R[0][1] = sin(alfa)*cos(beta);
R[1][1] = cos(alfa)*cos(gama) + sin(alfa)*sin(beta)*sin(gama);
R[2][1] = -cos(alfa)*sin(gama) + sin(alfa)*sin(beta)*cos(gama);
R[0][2] = -sin(beta);
R[1][2] = cos(beta)*sin(gama);
R[2][2] = cos(beta)*cos(gama);
}
void angle(float fi_b, float fi_p, float x, float y, float z)
{
bx = b*cos(fi_b);
by = b*sin(fi_b);
px = p*cos(fi_p);
py = p*sin(fi_p);
float A = R[0][0]*px + R[1][0]*py;
float B = R[0][1]*px + R[1][1]*py;
float C = R[0][2]*px + R[1][2]*py ;
A = A - bx + x;
B = B - by + y;
C = C + z;
float l = sqrt(A*A + B*B + C*C);
float L = l*l - s*s + a*a;
float M = 2*a*l;
float N = 2*a*(cos(fi_b)*(px - bx) + sin(fi_b)*(py - by));
angle0 = -(asin(L/(sqrt(M*M + N*N))) - atan(N/M));
}
void setup()
{
const char *log ;
Serial.begin(1000000);
uint16_t model_number1 = 1;
uint16_t model_number2 = 2;
uint16_t model_number3 = 3;
uint16_t model_number4 = 4;
uint16_t model_number5 = 5;
uint16_t model_number6 = 6;
dxl_wb.init(DEVICE_NAME, BAUDRATE, &log);
dxl_wb.ping(DXL_ID1, &model_number1, &log);
dxl_wb.ping(DXL_ID2, &model_number2, &log);
dxl_wb.ping(DXL_ID3, &model_number3, &log);
dxl_wb.ping(DXL_ID4, &model_number4, &log);
dxl_wb.ping(DXL_ID5, &model_number5, &log);
dxl_wb.ping(DXL_ID6, &model_number6, &log);
dxl_wb.jointMode(DXL_ID1, 20, 20, &log);
dxl_wb.jointMode(DXL_ID2, 20, 20, &log);
dxl_wb.jointMode(DXL_ID3, 20, 20, &log);
dxl_wb.jointMode(DXL_ID4, 20, 20, &log);
dxl_wb.jointMode(DXL_ID5, 20, 20, &log);
dxl_wb.jointMode(DXL_ID6, 20, 20, &log);
}
void loop()
{
if (Serial.available() > 0 ) {
x1 = Serial.parseInt();
y_1 = Serial.parseInt();
z1 = Serial.parseInt();
alfa1 = Serial.parseInt();
beta1 = Serial.parseInt();
gama1 = Serial.parseInt();
Serial.print(«X = « );
Serial.println(x1);
Serial.print(«Y = « );
Serial.println(y_1);
Serial.print(«Z = « );
Serial.println(z1);
Serial.print(«Alfa = « );
Serial.println(alfa1);
Serial.print(«Beta = « );
Serial.println(beta1);
Serial.print(«Gamma = « );
Serial.println(gama1);
alfa1 = alfa1*3.14/180;
beta1 = beta1*3.14/180;
gama1 = gama1*3.14/180;
matrix(alfa1, beta1, gama1);
angle(0.61, 0.13, x1, y_1, z1);
angle1 = angle0;
angle(1.48, 1.95, x1, y_1, z1);
angle2 = -angle0;
angle(2.7, 2.22, x1, y_1, z1);
angle3 = angle0;
angle(3.58, 4.04, x1, y_1, z1);
angle4 = -angle0;
angle(4.8, 4.31, x1, y_1, z1);
angle5 = angle0;
angle(5.6, 6.13, x1, y_1, z1);
angle6 = -angle0;
Serial.print(«Angle #1: « );
Serial.println(angle1);
Serial.print(«Angle #2: « );
Serial.println(angle2);
Serial.print(«Angle #3: « );
Serial.println(angle3);
Serial.print(«Angle #4: « );
Serial.println(angle4);
Serial.print(«Angle #5: « );
Serial.println(angle5);
Serial.print(«Angle #6: « );
Serial.println(angle6);
set_pos(angle1, angle2, angle3, angle4, angle5, angle6, 50);
}
}