Глава 2. Металлические манипуляторы

Угловой манипулятор

Рис. 2.1. Угловой манипулятор

Угловой манипулятор — это манипулятор с угловой кинематикой, предназначенный для поддержания, перемещения объектов в пространстве. Он может быть использован для перемещения объектов разного типа или для выполнения различных задач в области автоматизации процессов и робототехники.

Роботизированные манипуляторы широко используются в промышленности. Они выполняют задачи в фиксированной и изученной среде. Перемещаются в трех пространственных измерениях и имеют несколько осей вращения.

В манипуляторе можно выделить два участка кинематической цепи с различными функциями: механизм руки и механизм кисти. Под “рукой” понимают ту часть манипулятора, которая обеспечивает перемещение центра схвата; под “кистью” – те звенья и пары, которые обеспечивают ориентацию схвата.

Прямая кинематика спрашивает, где будет находиться захват после последовательности вращений сервоприводов манипулятора. Задачи обратной кинематики спрашивает, какие повороты сервоприводов приведут захват в заданное положение. Вращение манипулятора описывается матрицей вращения, элементы которой являются тригонометрическими функциями угла поворота.

Расчеты

Проведем оценку грузоподъемности робота. В рассматриваемой модели манипулятора применяются сервоприводы DYNAMIXEL XL431- T250-T и сервоприводы AR-S430-01, производимые OOO “Прикладная робототехника”. Их технические характеристики известны. Зная максимальный момент сервопривода, а также длины элементов конструкции модели, можно сделать расчет максимальной массы нагрузки, которую сможет поднять манипулятор.

В документации на сервоприводы можно найти, что максимальный момент, при котором сервоприводы способны к плавному и точному перемещению нагрузки – 0,53 Н∙м, а максимальный момент, который могут удерживать сервоприводы – 1,4 Н∙м.

Используя эти данные, рассчитаем массу полезной нагрузки для 2-го сервопривода в статическом положении, поскольку он является самым нагруженным из всех сервоприводов манипулятора. Первая степень в расчетах не учитывается, так как ось вращения вертикальна. Второму сервоприводу, помимо массы груза, также требуется перемещать массу всей конструкции манипулятора, которая расположена после него – то есть, 5 звеньев и 4 сервопривода. Расчет будем проводить для самой нагруженной конфигурации манипулятора для второго сервопривода – горизонтального положения, параллельно поверхности (рис. 2.2.)

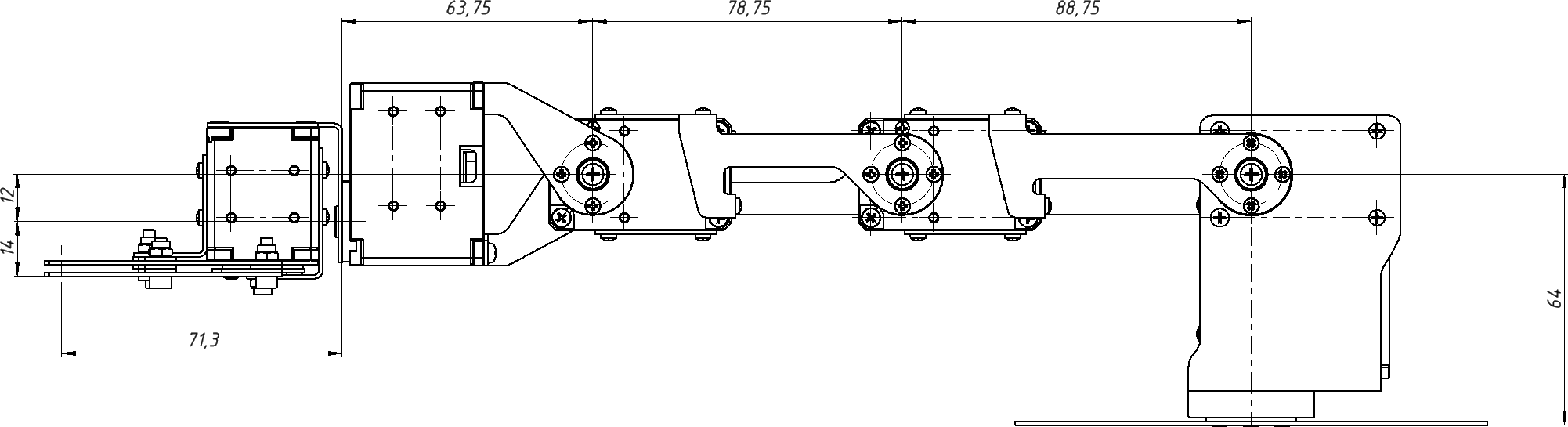
Рис. 2.2. Максимально нагруженное положение манипулятора

Формула для вычисления момента нагрузки на второе звено:

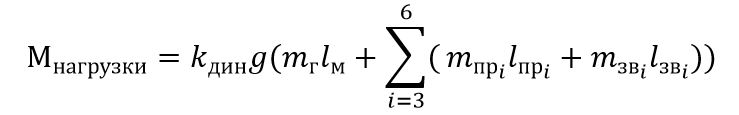
$K_{дин}$ -коэффициент динамики. Расчет производится для статического положения манипулятора, однако требуется учитывать динамические нагрузки. Стандартное значение k_дин = 1,4;

$g$ - ускорение свободного падения;

$m_r$ - масса груза;

$l_m$ - расстояние до центра масс зацепа груза;

$m_{пр_i}$ - масса i-го сервопривода;

$l_{пр_i}$ - расстояние до центра масс i-го сервопривода;

$m_{зв_i}$масса i-го звена манипулятора;

$l_{зв_i}$расстояние до центра масс i-го звена манипулятора.

Примем расстояние до захватываемого груза равным 302,55 мм – длина от оси вращения второго сочленения до окончания схвата манипулятора.

$\displaystyle\sum_{i=3}^{6} m_{пр_i}$= 228 грамм - суммарная масса сервоприводов.

Для упрощения решения задачи будем считать, что центр масс сервопривода располагается в центре вала вращения. Таким образом, найдем плечо до каждого сервопривода от оси вращения второго сочленения (рис. 2.2.).

Необходимую массу звеньев и центра масс узнаем с помощью 3D модели.

Масса звеньев робота зависит от формы, используемых материалов и технологии изготовлении. В случае использования стандартной модели звеньев манипулятора суммарная масса составит:

$\displaystyle\sum_{i=3}^{6} m_{зв_i}$= 140 грамм.

Центр масс, учитывающий звенья третьей, четвертой, пятой и шестой степени свободы, располагается на расстоянии 185,5 мм от оси вращения второго сервопривода.

Для нахождения массы груза, с которым манипулятор имеет возможность взаимодействовать, составим уравнение: $$ M_{нагрузки}=M_{серв} $$ Таким образом, момент $M_{нагрузки}$ создаваемый нагрузкой на второе сочленение, равняется моменту сервопривода $M_{серв}$ .

Из электромеханической характеристики сервопривода найдем крутящий момент:

\[M_{серв}=1,4Нм\]

Приведем известные значения к системе СИ и подставим в формулу:

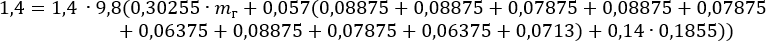
Преобразуем значения:

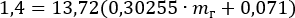
Выразим и найдем массу груза

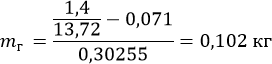
Таким образом, максимальная масса груза для обеспечения нормальной работы манипулятора составляет 102 грамм. Однако, это приблизительный расчет, так как исследовалось статическое и наиболее нагруженное положение манипулятора.

Delta-манипулятор

Манипулятор с Delta-кинематикой – вид параллельного робота, который состоит из трёх рычагов, прикреплённых посредством карданных шарниров к основанию. Ключевой особенностью является использование параллелограммов в конструкции манипулятора, что позволяет сохранять пространственную ориентацию исполнительного устройства робота.

Роботы с Delta-кинематикой (Delta-роботы) особенно популярны на линиях упаковки, поскольку они достаточно быстры. Некоторые осуществляют до 300 захватов в минуту. Delta-робота придумал в начале 1980-х годов швейцарский учёный Реймонд Клавель. Ниже приведена иллюстрация из оригинального патента US4976582 на «Устройство для перемещения и позиционирования элемента в пространстве» (Рис. 2.3).

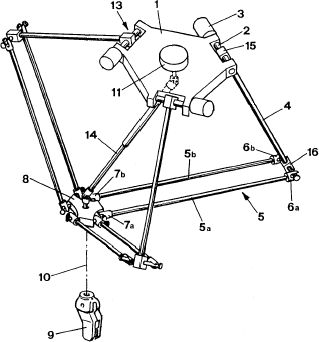
Рис. 2.3. Схемотехническое изображение Delta-робота

Робот состоит из двух платформ: неподвижно закреплённого верхнего основания

(1) и небольшой подвижной платформы (8), соединённых тремя рычагами. Каждый рычаг состоит из двух частей: верхнее плечо

(4) жёстко соединено с двигателем (3), расположенным на верхнем основании, а нижнее представляет собой параллелограмм (5), в углах которого установлены так называемые универсальные

шарниры (6, 7), которые позволяют углам изменяться. Каждый параллелограмм соединён с верхним рычагом шарниром (16) таким образом, чтобы его верхняя сторона всегда оставалась перпендикулярной своему рычагу и параллельной плоскости верхнего основания. Благодаря этому, подвижная платформа робота, прикреплённая к нижним сторонам параллелограммов, так же будет всегда параллельной верхнему основанию. Управлять положением платформы становится возможным, изменяя угол поворота верхних рычагов относительно основания робота при помощи двигателей. В центре нижней платформы (8) крепится рабочий

орган робота (9). Это может быть манипулятор, захватывающее устройство или, например, экструдер (в случае 3D принтера). Дополнительно может использоваться ещё один двигатель (11), который обеспечивает вращение рабочего органа через штангу (14). Тяжёлые двигатели размещены на неподвижном основании, движутся только рычаги и нижняя платформа, которые стараются изготавливать из лёгких композитных материалов, тем самым уменьшая их инерцию.

Обратная задача кинематики Delta-манипулятора

Для корректного управления Delta-манипулятором, необходимо научиться решать обратную (инверсную) кинематическую задачу. Исходя из известной позиции, в которую требуется переместить манипулятор робота (например, схватить объект, который находится на конвейере в точке с координатами x, y, z), требуется определить величины углов, на которые необходимо повернуть двигатели, связанные с рычагами робота, чтобы установить его в правильное положение для захвата.

Формализованная задача выглядит следующим образом: неподвижное основание робота и его движущуюся платформу можно представить в виде равносторонних треугольников. На представленной ниже схеме они закрашены зелёным и розовым цветами, соответственно. Углы поворота рычагов робота относительно плоскости основания (они же — углы поворота моторов) обозначены как

$θ_1$ $θ_2$ $θ_3$

а координаты точки E0, расположенной в центре подвижной платформы, и в которой в реальной жизни будет закреплён манипулятор — как

($x_0$ , $y_0$ , $z_0$ )

Таким образом, необходимо придумать функцию для решения обратной кинематической задачи:

$f_{inverse}(x_0,y_0,z_0) -> (θ_1,θ_2,θ_3)$

Зададим несколько ключевых параметров, которые определяются геометрическими размерами нашего робота (Рис. 2.4).

Обозначим длину стороны верхнего основания f, сторону нижней платформы e, длину верхнего плеча рычага rf и длину нижнего плеча (длинной стороны параллелограмма) re. Для вычислений выберем систему координат с точкой отсчёта, совпадающей с геометрическим центром верхнего треугольника. Ось Z направим вверх, таким образом, z-координата подвижной платформы всегда будет отрицательной.

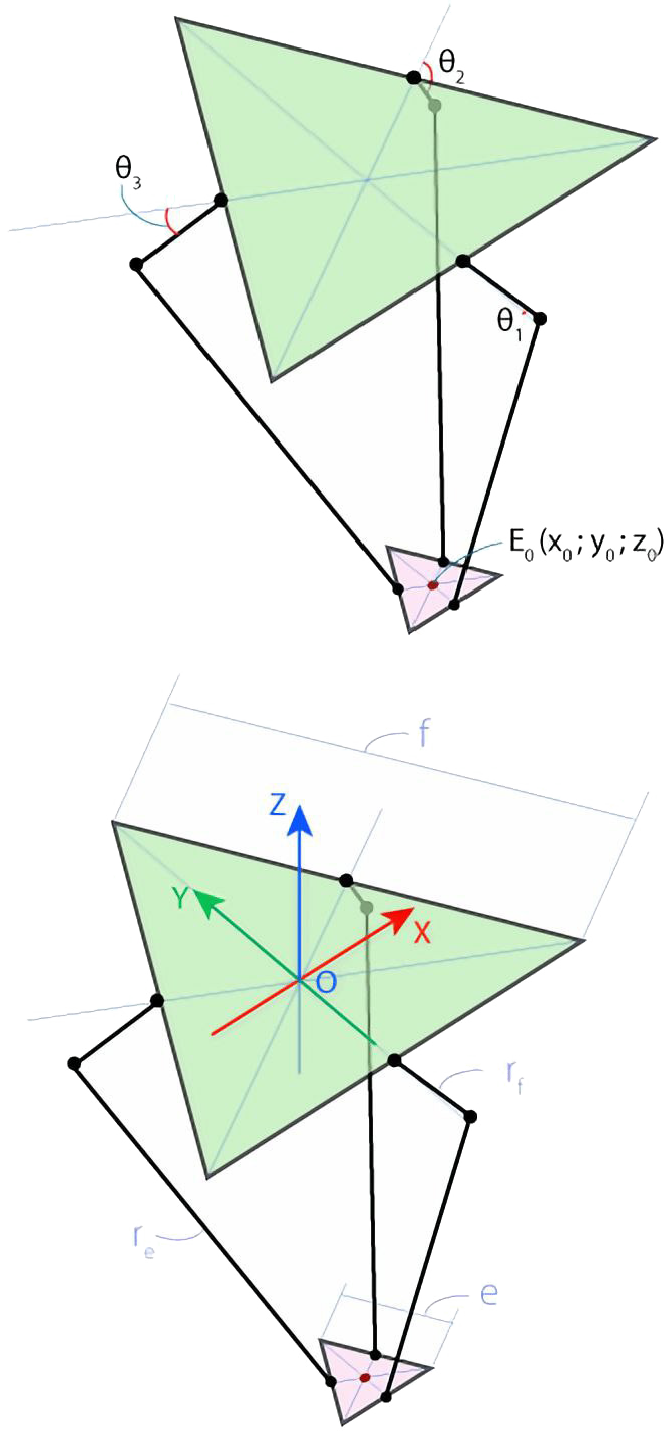Рис. 2.4. Схематические изображения Delta-робота для решения обратной кинематической задачи

Конструкция робота подразумевает, что рычаг $F_1$ $J_1$ *(Рис. 2.5) может вращаться лишь в плоскости $YZ$, описывая при этом окружность радиусом $rf$ с центром в точке $F_1$ (именно в этом месте он прикреплён к двигателю). В отличие от $F_1$, в узлах $J_1$ и $E_1$ используются универсальные шарниры, благодаря которым плечо $E_1$$J_1$ может свободно вращаться относительно $J_1$, описывая сферу радиусом $re$ с центром в точке $E_1$.

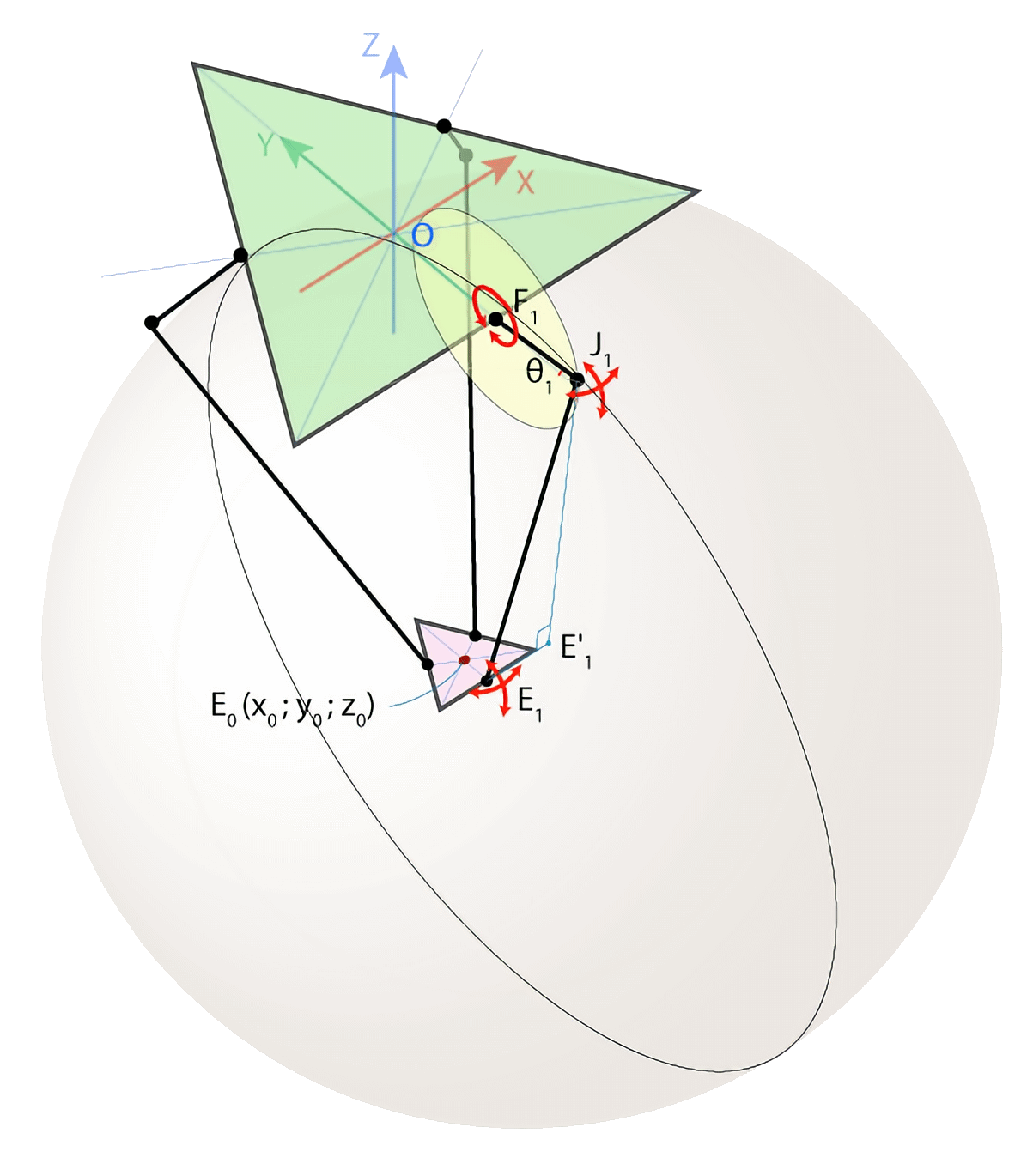
Рис. 2.5. Схематические изображения Delta-робота для решения обратной кинематической задачи

Пересечением этой сферы и плоскости $YZ$ *является окружность с центром в точке $E’_1$ радиусом $E’_1J_1$ где точка $E’_1$ находится как проекция точки $E’_1$ на плоскость $YZ$. Тогда точка $J_1$ будет находиться на пересечении двух окружностей с центрами в точках $E’_1$ и $F_1$, причём радиусы этих окружностей мы можем определить. Здесь присутствует небольшая тонкость: окружности пересекаются в двух точках, но нас интересует только одна из них — с меньшим значением координаты y, поскольку мы хотим, чтобы рычаги робота всегда торчали «локтями» наружу. Определив таким образом координаты точки $J_1$, мы легко сможем найти интересующий нас угол $θ_1$

Для удобства восприятия ниже показана проекция нашей

трёхмерной картинки на плоскость $YZ$ (Рис. 2.6).

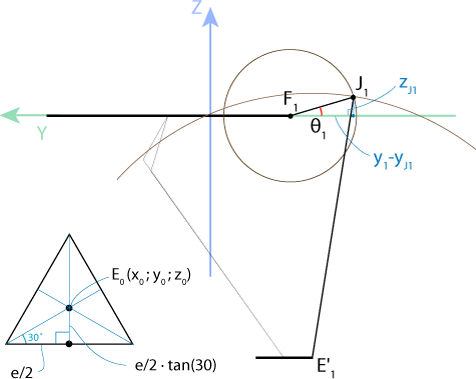
Рис. 2.6. Проекция трехмерного схематического изображения Delta-робота на плоскость YZ

Нижняя платформа равносторонний треугольник, центром которого является точка

$E_0 (x_0 , y_0 , z_0 )$

Значит, расстояние $E_0$$E_1$ можно рассчитать по следующей формуле:

\[ E_0E_1=\frac e2 \tan (30)=\frac {e}{2\sqrt{3}} \]

что даёт нам следующие координаты точки $E_1$ и её проекции $E’_1$ на плоскость $YZ$:

\[ E_1(x_0,y_o- \frac{e}{2 \sqrt 3}, z_0) => E’_1(0,y_o- \frac{e}{2 \sqrt 3}, z_0) \]

Расстояние $E_1E’_1=x_0$, тогда, согласно теореме Пифагора:

$$ E'_1j_1= \sqrt{E_1j^2_1-E_1E'^2_1}=\sqrt{r^2_e-x^2_0} $$ Поскольку верхняя платформа также является равносторонним треугольником, то координаты точки $F_1$ будут:

\[ F_1(0,\frac{-f}{2\sqrt{3}},0) \]

Чтобы найти координаты точки $J_1$, являющейся пересечением двух окружностей, надо решить систему уравнений:

\[ \begin{cases} (y_{J_1}-y_{F_1})^2+(z_{J_1}-z_{F_1})^2=r^2_f \\ (y_{J_1}-y_{E_1})^2+(z_{J_1}-z_{E_1})^2=r^2_e-x^2_0 \end{cases} \]

Координаты центров окружностей нам известны. Если подставить их в систему уравнений, получатся следующие выражения:

\[ \begin{cases} (y_{J_1}+\frac {f}{2\sqrt3})^2+z_{J_1}^2=r^2_f \\ (y_{J_1}-y_{0}+\frac{e}{2\sqrt3})^2+(z_{J_1}-z_{0})^2=r^2_e-x^2_0 \end{cases} \]

После раскрытия скобок и вычитания одного уравнения из другого, можно линейным образом выразить z-координату точки J1 через y-координату:

$z_{j_1}=a+b+y_{J_1}$ , где

$a=(r^2_f-r^2_e+x^2_0+y^2_0+z^2_0-\frac{e}{2\sqrt3}+\frac{f}{2\sqrt3})*\frac{1}{2_{z_0}}$ $b=(\frac{e}{2sqrt3}-y_0-\frac{f}{2\sqrt3})*\frac{1}{z_0}$

Подставив определенную выше z-координату во второе уравнение, получим обычное квадратное уравнение относительно y. Из двух решений уравнения выберем наименьшее (как это обсуждалось выше). Получив таким образом координаты точки J1, найдём и угол:

\[ θ_1=arctan(\frac{z_{j_1}}{y_{F_1}-y_{J1}}) \]

Все выражения получились достаточно простыми благодаря удачному выбору системы координат: плечо рычага F1J1 всегда движется в плоскости YZ, поэтому координату x можно просто не учитывать. Чтобы сохранить это преимущество при нахождении двух оставшихся углов Θ2 и Θ3, воспользуемся симметрией конструкции Delta-робота. Сначала повернём нашу систему координат на 120° против часовой стрелки в плоскости XY вокруг оси Z (Рис.2.7).

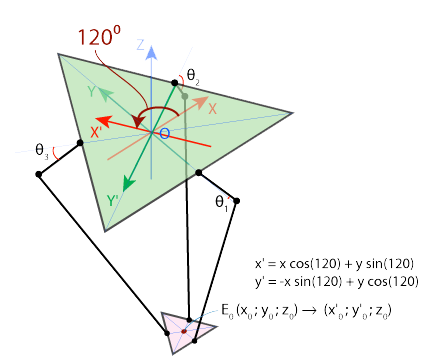
Рис. 2.7. Поворот системы координат на 120 градусов вокруг оси Z в плоскости XY

В результате получается новая система координат X’Y’Z’, и в этой новой системе можно воспользоваться готовыми формулами для нахождения угла Θ2. Единственная тонкость заключается в том, что необходимо предварительно пересчитать координаты точки E0 в новой системе отсчёта. Это легко сделать при помощи известной формулы (преобразования при повороте системы вокруг начала координат), показанной на рисунке выше. Для нахождения угла Θ3 необходимо будет также повернуть исходную систему отсчёта, но теперь уже по часовой стрелке. Этот приём очень удобно реализуется в виде программы: достаточно написать функцию для вычисления угла Θ в плоскости YZ, а затем вызвать её три раза для каждого из углов и систем отсчёта.

Устройство Delta-манипулятора

Рис. 2.8. Собранный манипулятор с Delta-кинематикой

Инструкция по сборке робота, а также исходные файлы конструктивных элементов под лазерную резку находятся в свободном доступе и доступны для скачивания с официального сайта appliedrobotics.ru из раздела «Учебные материалы». На верхней неподвижной платформе установлено три сервопривода AR-S430-01. В качестве управляющей платы используется аппаратная платформа OpenCM со встроенным микроконтроллером STM. Также используется плата расширения STEM Board и встраиваемый одноплатный компьютер NanoPi-AR. Питание обеспечивается при помощи стандартного LiPo аккумулятора, выдающего номинальное напряжение в 11,1 В, либо через сетевой адаптер питания. Соединение сервоприводов рекомендуется выполнить последовательно и подключить получившуюся цепь к плате расширения STEM Board:

Рис. 2.9. Схема подключения сервоприводов

Перед тем как приступить к разработке управляющей программы, необходимо проверить ID сервоприводов, установленных на манипуляторе. ID сервоприводов указаны на следующей схеме:

Рис. 2.10. Схема назначения ID сервоприводов

Для проверки и установки ID сервоприводов можно использовать стандартные примеры из Arduino IDE с установленной поддержкой платы OpenCM9.04. Для этого необходимо открыть два примера под названием: “o_Find_Dynamixel” и “c_ID_Change”. (“Файл“ => “Примеры“ => OpenCM9.04 => DynamixelWorkbench).

С помощью примера “o_Find_Dynamixel” можно узнать текущее ID сервопривода: сервопривод подключается к плате, подаётся питание, и загружается пример на плату. После чего в Мониторе порта Arduino IDE выводится информация о текущем значении ID, которое необходимо запомнить.

После этого откройте второй пример - “c_ID_Change”. В оглавлении, при необходимости, требуется изменить строки:

#define DXL_ID 1 // 1 – текущее значение ID сервопривода #define NEW_DXL_ID 2 // 2 – требуемое значение ID сервопривода

Помимо этого, необходимо поменять скорость передачи данных #define BAUDRATE 57600 // изменяем значение на 1 000 000

Таким образом, устанавливаются необходимые ID.

Для обеспечения безопасной работы, рекомендуется перед запуском определить, в каком положении находится вал сервопривода при 0°.

Разработка управляющей программы

В модели данного робота в качестве управляющего контроллера используется OpenCM. Для работы используется среда разработки Arduino IDE.

Для работы с сервоприводами DYNAMIXEL необходимо подключить библиотеку и инициализировать переменные:

#include <DynamixelWorkbench.h> DynamixelWorkbench dxl_wb;

Для обмена данных по протоколу Dynamixel в коде программы необходимо указать номер аппаратной шины.

#define Device_Name “1” – подключение к порту на плате OpenCM9.04

#define Device_Name “2” – подключение через USB переходник или через Bluetooth

#define Device_Name “3” – подключение к плате расширения STEM Board

В рассматриваемом примере используется третий вариант

Указывается скорость обмена данными через порт подключения: #define BAUDRATE 1000000

Далее требуется указать ID сервоприводов, которыми используются в работе.

#define DXL_ID1 1

#define DXL_ID2 2

#define DXL_ID3 3 // Объявление ID сервоприводов манипулятора (1-3)

Также инициализируются геометрические данные Delta-робота в качестве глобальных переменных. Они необходимы для расчетов. В рассматриваемой модели робота нужно инициализировать следующие переменные:

int f = 208; 
int Rf = 90; 
int Re = 168; 
int e = 52;

float theta1, theta2, theta3, theta ; // Угол поворота вала двигателя 
float y_1, y_2, y_3;

float x_1, x_2, x_3; 
float m, n, k;

Функция setup()

Создаем переменные «model_number» и присваиваем им номер сервопривода. После производим подключение всех сервоприводов манипулятора.

Записываем функцию инициализации:

dxl_wb.init(DEVICE_NAME, BAUDRATE, &log); 
Serial.begin(1000000);


const char *log ;

uint16_t model_number1 = 1; 
uint16_t model_number2 = 2; 
uint16_t model_number3 = 3;

dxl_wb.ping(DXL_ID1, &model_number1, &log); 
dxl_wb.ping(DXL_ID2, &model_number2, &log); 
dxl_wb.ping(DXL_ID3, &model_number3, &log);

Настройка режима работы сервоприводов в качестве шарниров:

dxl_wb.jointMode(DXL_ID1, 50, 0, &log);

dxl_wb.jointMode(DXL_ID2, 50, 0, &log);

dxl_wb.jointMode(DXL_ID3, 50, 0, &log);

Где значение 50 является скоростью, а 0 – ускорение. Теперь рассмотрим действие каждой функции отдельно.

Функция coord()

В этой функции осуществляется пересчёт координат точки Е0 в других системах отсчёта.

void coord(float a, float b)

{

x1 = a; // координаты первой точки 
y1 = b;

x2 = a*cos(2.094) + b*sin(2.094); // координаты второй точки 
y2 = b*cos(2.094) - a*sin(2.094);

x3 = a*cos(2.094) - b*sin(2.094); // координаты третьей точки 
y3 = b*cos(2.094) + a*sin(2.094);

}

Функция find_angle()

В этой функции решается обратная задача кинематики: рассчитывается дискриминант, проверяется его не отрицательность, производится нахождение корней и угла.

void find_angle(float x, float y, float z)

{

float C1 = -0.5 * 0.57735 * f; // f/2 * tg 30 y -= 0.5 * 0.57735 * e;

float a = (x*x + y*y + z*z +Rf*Rf - Re*Re - C1*C1)/(2*z); 
float b = (C1-y)/z;

float d = -(a+b*C1)*(a+b*C1)+Rf*(b*b*Rf+Rf); if(d < 0) // проверка дискриминанта

Serial.println(«Error»);

float yj = (C1 - a*b - sqrt(d))/(b*b + 1); // выбираем внешнюю точку 
float zj = a + b*yj;

float angle = atan(-zj/(C1 - yj)); 
theta = angle;

}

Функция full()

В этой функции осуществляется нахождение трех углов для каждого двигателя.

void full(float x0, float y0, float z0)

{

// Рассчитаем в какую точку переместится манипулятор при введенных координатах.

coord(x0, y0); // Расчёт координат каждой точки 
find_angle(x_1, y_1, z0); // Расчёт угла для первого двигателя 
theta1 = theta;

find_angle(x_2, y_2, z0); // Расчёт угла для второго двигателя 
theta2 = theta;

find_angle(x_3, y_3, z0); // Расчёт угла для третьего двигателя 
theta3 = theta;

}

Функция set_pos()

В данной функции осуществляется задание угла поворота вала двигателя на манипуляторе.

void set_pos( float p1, float p2, float p3, int del) // Поворот задается в радианах, del – задержка

{

dxl_wb.goalPosition(DXL_ID1,p1); 
dxl_wb.goalPosition(DXL_ID2,p2); 
dxl_wb.goalPosition(DXL_ID3,p3); 
delay(del);

}

Функция loop()

Данная функция представляет собой бесконечный цикл. Например, переместим нижнюю платформу манипулятора в координаты х = 0; у = 0; z = -100;

void loop()

{

full(0,0,-100);

set_pos(theta1, theta2, theta3, 500); // Поворот валов сервоприводов на вычисленный угол – достижение заданных координат

}

// Также можно корректировать положения робота в реальном времени. С помощью консоли пользователь может вводить координаты, и робот будет их занимать.

// Редактируем функцию loop():

if (Serial.available() > 0 ) // Функция, проверяющая наличие символов, введенных в консоль

{

m = Serial.parseInt(); // Присваивание глобальной переменной первое целочисленное значение

n = Serial.parseInt(); 
k = Serial.parseInt();

Serial.print(«X = « ); // Вывод координат, введённых пользователем

Serial.println(m); 
Serial.print(«Y = « ); 
Serial.println(n); 
Serial.print(«Z = « ); 
Serial.println(k);

full(m, n, k); // Расчет углов поворота для введенных координат Serial.print(«Angle #1: « ); // Вывод угла поворота первого двигателя

Serial.println(theta1); 
Serial.print(«Angle #2: « ); 
Serial.println(theta2); 
Serial.print(«Angle #3: « ); 
Serial.println(theta3);

set_pos(theta1, theta2, theta3, 500); // Поворот на вычисленный угол

}

}

Значения можно вводить через любые знаки препинания, главное в правильном порядке, и разделять их пробелом.

В результате, код управляющей программы будет выглядеть следующим образом:

#include <DynamixelWorkbench.h> 
#if defined( OPENCM904 )
#define DEVICE_NAME «3» // Сервопривод на SERIAL3(USART3)<--- STEM BOARD
#elif defined( OPENCR ) 
#define DEVICE_NAME «» 
#endif

#define BAUDRATE 1000000

#define DXL_ID1 1

#define DXL_ID2 2

#define DXL_ID3 3 
DynamixelWorkbench dxl_wb;

int f = 208; 
int Rf = 90; 
int Re = 168; 
int e = 52;

float theta1, theta2, theta3, theta; 
float y_1, y_2, y_3;

float x_1, x_2, x_3; 
float m, n, k;

void coord(float a, float b)

{

x_1 = a; y_1 = b;

x_2 = a*cos(2.094) + b*sin(2.094); 
y_2 = b*cos(2.094) - a*sin(2.094); 
x_3 = a*cos(2.094) - b*sin(2.094); 
y_3 = b*cos(2.094) + a*sin(2.094);

}

void find_angle(float x, float y, float z)

{

float C1 = -0.5 * 0.57735 * f; // f/2 * tg 30

y -= 0.5 * 0.57735 * e;

float a = (x*x + y*y + z*z +Rf*Rf - Re*Re - C1*C1)/(2*z); 
float b = (C1-y)/z;
float d = -(a+b*C1)*(a+b*C1)+Rf*(b*b*Rf+Rf); 

if(d < 0)

Serial.println(«Error»);

float yj = (C1 - a*b - sqrt(d))/(b*b + 1); 
float zj = a + b*yj;

float angle = atan(-zj/(C1 - yj)); 
theta = angle;

}

void full(float x0, float y0, float z0)

{

coord(x0, y0); 
find_angle(x_1, y_1, z0); 
theta1 = theta; 
find_angle(x_2, y_2, z0); 
theta2 = theta; 
find_angle(x_3, y_3, z0); 
theta3 = theta;

}

void set_pos( float p1 , float p2, float p3, int del)

// функция для задания угла поворота вала двигателя на манипуляторе в радианах

{

dxl_wb.goalPosition(DXL_ID1,p1); 
dxl_wb.goalPosition(DXL_ID2,p2); 
dxl_wb.goalPosition(DXL_ID3,p3); 
delay(del);

}

void setup()

{

const char *log ; 
Serial.begin(9600);

uint16_t model_number1 = 1; 
uint16_t model_number2 = 2; 
uint16_t model_number3 = 3;

dxl_wb.init(DEVICE_NAME, BAUDRATE, &log); 
dxl_wb.ping(DXL_ID1, &model_number1, &log);

dxl_wb.ping(DXL_ID2, &model_number2, &log); 
dxl_wb.ping(DXL_ID3, &model_number3, &log); 
dxl_wb.jointMode(DXL_ID1, 50, 0, &log);

dxl_wb.jointMode(DXL_ID2, 50, 0, &log);

dxl_wb.jointMode(DXL_ID3, 50, 0, &log);

}

void loop() {

if (Serial.available() > 0 ) {

m = Serial.parseInt();

n = Serial.parseInt(); 
k = Serial.parseInt(); 
Serial.print(«X = « ); 
Serial.println(m); 
Serial.print(«Y = « ); 
Serial.println(n); 
Serial.print(«Z = « ); 
Serial.println(k); 
full(m, n, k);

Serial.print(«Angle #1: « ); 
Serial.println(theta1); 
Serial.print(«Angle #2: « ); 
Serial.println(theta2); 
Serial.print(«Angle #3: « ); 
Serial.println(theta3); 
set_pos(theta1, theta2, theta3, 500);

}

}

Техническое зрение

Функционал Delta-манипулятора может быть расширен за счет применения модуля технического зрения TrackingCam, способного выполнять анализ объектов и различать их по цвету и форме. Модуль технического зрения TrackingCam входит в состав образовательного набора.

Настройка модуля технического зрения TrackingCam.

В данном примере модуль технического зрения должен отслеживать объекты, попадающие как в зону видимости камеры, так и в рабочую зону манипулятора, и имеющие разный цвет. Будем использовать камеру, расположенную перпендикулярно к рабочей плоскости манипулятора. Прикрепим камеру (Рис. 2.11)

Рис. 2.11. Установленный модуль технического зрения на Delta-манипулятор

Поскольку модуль технического зрения закрепляется не четко по центру манипулятора, у него наблюдается смещение зоны видимости, относительно рабочей зоны манипулятора (Рис. 2.12).

|300 |300

Рис. 2.12. Соотношение зоны видимости камеры и рабочей зоны манипулятора

Чтобы модуль мог распознать объект и передать контроллеру информацию о его положении, его нужно предварительно настроить. Для этого необходимо воспользоваться утилитой TrackingCam App, при помощи которой модулю можно задать цветовые и морфологические признаки объекта, настроить параметры порта ввода-вывода информации и сохранить настройки (см. учебное пособие «Техническое зрение роботов с использованием TrackingCam») (Рис. 2.13). Желательно выбрать объекты контрастных цветов и контрастный фон.

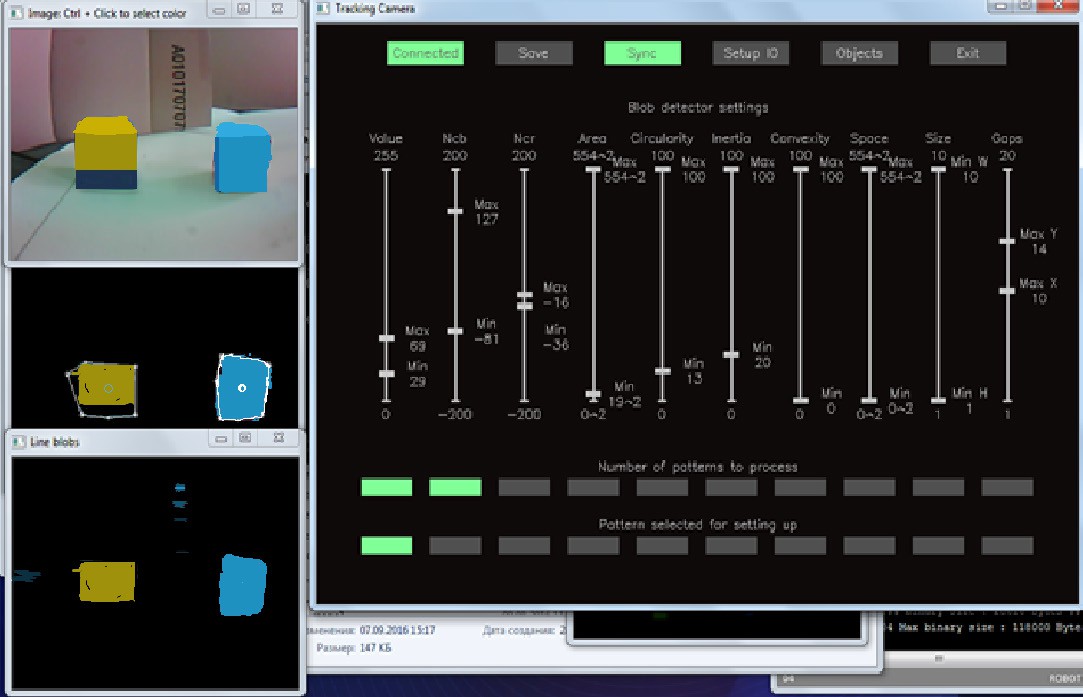
Рис. 2.13. Интерфейс настройки модуля технического зрения

После сохранения настроек модуля перейдем к подключению. Подключение модуля технического зрения TrackingCam осуществляется как обычное Dynamixel-совместимое устройство, поэтому можно подключить модуль последовательно к сервоприводам.

Система отсчета

Проблема ориентации камеры и манипулятора заключается в том, что координатные оси устройств не совпадают.

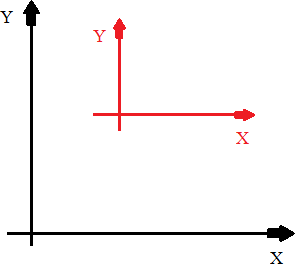
Рис. 2.14. Несовпадение осей ориентации камеры и манипулятора

Красным выделены оси камеры, черным – манипулятора.

Для начала узнаем координаты нулевой точки манипулятора для системы координат камеры. Поставим предмет, на который мы настроили модуль технического зрения, в центр (нулевая точка манипулятора). А в утилите TrackingCam App нажмем на окно, где отображается центр опознанного объекта. Таким образом, программа сообщит нам координаты этого объекта для камеры модуля – (X,Y). Модуль технического зрения выдает различные данные. В данном случае нас интересует лишь значения по оси Х и оси Y. Таким же способом можно узнать координаты объекта в другом положении на плоскости $(S_1 , S_2)$.

Теперь осуществим перенос центр системы координат камеры в центр системы координат манипулятора и найдем координаты объекта в новой системе.

$X_1 := X - S_1$

$Y_1 := Y - S_2$

где $S_1$ и $S_2$- текущие координаты предмета.

В данном примере рассматривается простейший случай переноса системы координат. Он охватывает базовый вариант переноса системы координат, который включает сравнительно простой способ изменения начала координат в трехмерном пространстве. Эта операция выполняется с целью улучшения удобства расчетов и анализа в зависимости от решаемой задачи, связанные с трехмерными моделями.